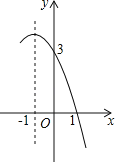题目内容
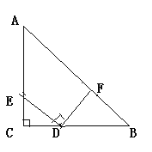
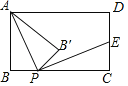
【题目】如图,矩形ABCD中,AB=2,BC=4,点P是BC边上的一个动点(点P不与点B,C重合),现将△ABP沿直线AP折叠,使点B落到点B′处;作∠B′PC的角平分线交CD于点E.设BP=x,CE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.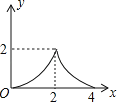 B.
B.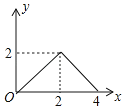
C.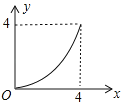 D.
D.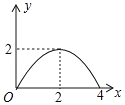
【答案】D
【解析】
根据折叠可证明△ABP∽△PCE,得![]() ,进而可得函数解析式y=
,进而可得函数解析式y=![]() x(4﹣x)=﹣
x(4﹣x)=﹣![]() x2+2x,即可判断函数图象.
x2+2x,即可判断函数图象.
∵△ABP沿直线AP折叠得到△AB′P,
∴∠APB=∠APB′,
∵PE平分∠B′PC,
∴∠B′PE=∠CPE,
∴∠APB′+∠EPB′=![]() ×180°=90°,
×180°=90°,
∵∠C=90°,
∴∠CPE+∠CEP=90°,
∴∠APB=∠CEP,
∵∠B=∠C=90°,
∴△ABP∽△PCE,
∴![]() ,
,
∵BP=x,CE=y,矩形ABCD中,AB=2,BC=4,
∴PC=4﹣x,
∴![]()
∴y=![]() x(4﹣x)=﹣
x(4﹣x)=﹣![]() x2+2x.
x2+2x.
∴该函数图象是抛物线,开口向下.
故选:D.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
【题目】已知函数![]() ,其自变量的取值范围是x>-2,当x=2时,y1=-2;当x=6时,y1=-5.
,其自变量的取值范围是x>-2,当x=2时,y1=-2;当x=6时,y1=-5.
(1)根据给定的条件,求出a、b的值和y1的函数解析式;
(2)根据你所求的函数解析式,选取适当的自变量x完成下表,并在下面的平面直角坐标系中描点并画出函数的大致图象.
x | … | 6 | … | |||||||
y | … | -5 | … |
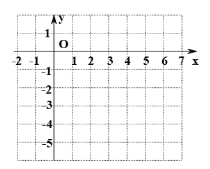
(3)请画出y2=x-4的图象,并结合图象直接写出:当y1>y2时,x的取值范围是 .