题目内容
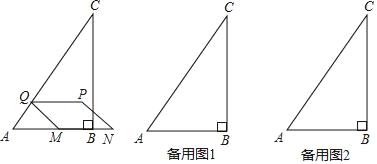
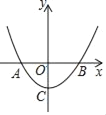
【题目】如图,二次函数y=x2﹣m2(m>0且为常数)的图象与x轴交于点A、B(A在B左侧),与y轴交于C.
(1)求A,B,C三点的坐标(用含m的式子表示);
(2)若∠ACB=90°,求m的值.
【答案】(1) A(﹣m,0),B(m,0),C(0,﹣m2);(2) m的值为1.
【解析】
(1)令y=0,解方程x2﹣m2=0,可求出点A和点B的坐标;令当x=0,解方程x2﹣m2=0,可求出点C的坐标;
(2)由∠ACB=90°及二次函数的对称性可证明△BOC是等腰直角三角形,从而可得m2=m,进而可求出m的值.
(1)当y=0时,x2﹣m2=0,解得x1=﹣m,x2=m,则A(﹣m,0),B(m,0),
当x=0时,y=x2﹣m2=﹣m2,则C(0,﹣m2);
(2)∵∠ACB=90°,OC⊥AB,OA=OB,
∴∠CBO=45 ,
∴△BOC是等腰直角三角形,
∴OC=OB,
∴m2=m,解得m1=0(舍去),m2=1,
∴m的值为1.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目