题目内容
【题目】如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M,B,C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y. 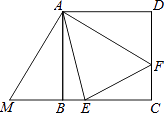
(1)图中△ADF可以绕点按顺时针方向旋转°后能与△重合;
(2)用x、y的代数式表示△AEM与△EFC的面积.
【答案】
(1)A;90°;ABM
(2)解:∵△AEM与△AEF恰好关于所在直线成轴对称,
∴EF=EM,
即x=BE+BM,
∵BM=DF,
∴x=DF+BE,
∴S△AME= ![]() ABME=
ABME= ![]() xy,
xy,
S△CEF=S正方形ABCD﹣S△AEF﹣S△ABE﹣S△ADF
=y2﹣ ![]() xy﹣
xy﹣ ![]() yBE﹣
yBE﹣ ![]() yDF
yDF
=y2﹣ ![]() xy﹣
xy﹣ ![]() y(BE+DF)
y(BE+DF)
=y2﹣ ![]() xy﹣
xy﹣ ![]() yx
yx
=y2﹣xy
【解析】解:(1)图中△ADF可以绕点A按顺时针方向旋转90°后能够与△ABM重合; 所以答案是:A、90°,ABM.
【考点精析】解答此题的关键在于理解轴对称的性质的相关知识,掌握关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为了解居民用水情况,小明在某小区随机抽查了30户家庭的月用水量,结果如下表:
月用水量/m3 | 4 | 5 | 6 | 8 | 9 | 10 |
户数 | 6 | 7 | 9 | 5 | 2 | 1 |
则这30户家庭的月用水量的众数和中位数分别是( )
A.6,6
B.9,6
C.6,9
D.6,7
