Question

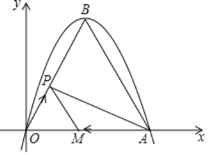
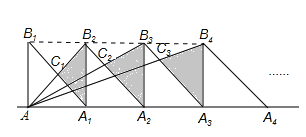
【题目】如图，7个腰长为1的等腰直角三角形(Rt△B1AA1，Rt△B2A1A2，Rt△B3A2A3…)有一条腰在同一条直线上，设△A1B2C1的面积为S1，△A2B3C2的面积为S2，△A3B4C3的面积为S3，则阴影部分的面积是______ .

Answer 1

【答案】

【解析】

连接B1、B2、B3、B4点，显然它们共线且平行于AC1，依题意可知△B1B2C1与△C1AA1相似，求出相似比，根据三角形面积公式可得出S1，同理：B2B3：AA2=1：2，所以B2C2：C2A=1：2，进而求出S2、 S3…S7，最后求和即可.

解：连接B1、B2、B3、Ba.

∵7个边长为1的等腰三角形有一条边在同一直线上，

∴ 连接B1、B2、B3点，显然它们共线且平行于AA1

∴S1=

∵B2B3∥AA2，

∴△B2C2B3∽△A2C2A，

∴

∴S2=SA2B3B2=×=

同理：S3= ×=，S4= ×=，S5= ×=，S6= ×=，S7= ×=，

∴阴影部分的面积为：++++++=