题目内容
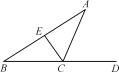
【题目】如图,CA平分∠DCE,且与BE的延长线相交于点A.
(1)若∠A=35°,∠B=30°,则∠BEC= ;(直接在横线上填写度数)
(2)小明经过改变∠A,∠B的度数进行多次探究,得出∠A,∠B,∠BEC三个角之间存在固定的数量关系,请你用一个等式表示出这个关系,并进行证明.
【答案】(1)100°;(2)∠BEC=2∠A+∠B,理由见解析
【解析】
(1)依据三角形外角性质,即可得到∠ACD=∠A+∠B=65°,依据AC平分∠DCE,可得∠ACE=∠ACD=65°,进而得出∠BEC=∠A+∠ACE=35°+65°=100°;
(2)依据AC平分∠DCE,可得∠ACD=∠ACE,依据三角形外角性质可得∠BEC=∠A+∠ACE=∠A+∠ACD,根据∠ACD=∠A+∠B,即可得到∠BEC=∠A+∠A+∠B=2∠A+∠B.
(1)∵∠A=35°,∠B=30°,
∴∠ACD=∠A+∠B=65°,
又∵AC平分∠DCE,
∴∠ACE=∠ACD=65°,
∴∠BEC=∠A+∠ACE=35°+65°=100°,
故答案为:100°;
解:∠BEC=2∠A+∠B.
证明:∵CA平分∠DCE,
∴∠ACD=∠ACE.
∵∠BEC=∠A+∠ACE=∠A+∠ACD,
∠ACD=∠A+∠B,
∴∠BEC=∠A+∠A+∠B=2∠A+∠B.

练习册系列答案
相关题目