题目内容
【题目】如图，在Rt△ABC中，∠C=90°，按下列步骤作图：①以点B为圆心，适当长为半径画弧，与AB，BC分别交于点D，E；②分别以D，E为圆心，大于
DE的长为半径画弧，两弧交于点P；③作射线BP交AC于点F；④过点F作FG⊥AB于点G．下列结论正确的是（ ）
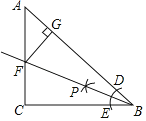
A. CF=FG B. AF=AG C. AF=CF D. AG=FG
【答案】A
【解析】
根据作图的过程知道：EF是∠CBG的角平分线，根据角平分线的性质解答．
解：根据作图的步骤得到：EF是∠CBG的角平分线，
A、因为EF是∠CBG的角平分线，FG⊥AB，CF⊥BC，所以CF=FG，故本选项正确；
B、AF是直角△AFG的斜边，AF＞AG，故本选项错误；
C、EF是∠CBG的角平分线，但是点F不一定是AC的中点，即AF与CF不一定相等，故本选项错误；
D、当Rt△ABC是等腰直角三角形时，等式AG=FG才成立，故本选项错误；
故选：A．
练习册系列答案
华东师大版一课一练系列答案
相关题目
