题目内容
【题目】已知非直角三角形ABC中,∠A=45°,高BD与高CE所在直线交于点H,则∠BHC的度数是____.
【答案】45°或135°
【解析】
①△ABC是锐角三角形时,先根据高线的定义求出∠ADB=90°,∠BEC=90°,然后根据直角三角形两锐角互余求出∠ABD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解;②△ABC是钝角三角形时,根据直角三角形两锐角互余求出∠BHC=∠A,从而得解.
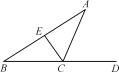
如图1,△ABC是锐角三角形时,
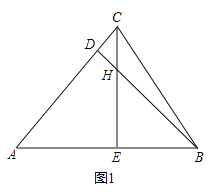
∵BD、CE是△ABC的高线,
∴∠ADB=90°,∠BEC=90°.
在△ABD中,∵∠A=45°,
∴∠ABD=90°-45°=45°,
∴∠BHC=∠ABD+∠BEC=45°+90°=135°;
②如图2,△ABC是钝角三角形时,
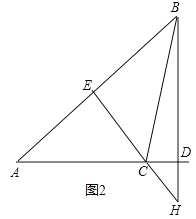
∵BD、CE是△ABC的高线,
∴∠A+∠ACE=90°,∠BHC+∠HCD=90°,
∵∠ACE=∠HCD(对顶角相等),
∴∠BHC=∠A=45°.
综上所述,∠BHC的度数是135°或45°.
故答案为:45°或135°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目