题目内容
【题目】如图,抛物线y=ax2+bx+c经过A(﹣1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于E.

(1)求抛物线的函数表达式;
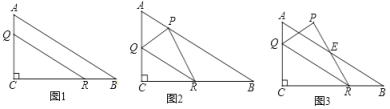
(2)如图1,求线段DE长度的最大值;
(3)如图2,设AB的中点为F,连接CD,CF,是否存在点D,使得△CDE中有一个角与∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2) 当a=2时,DE取最大值,最大值是
x+3;(2) 当a=2时,DE取最大值,最大值是![]() ;(3)存在点D,使得△CDE中有一个角与∠CFO相等,点D的横坐标为
;(3)存在点D,使得△CDE中有一个角与∠CFO相等,点D的横坐标为![]() 或
或![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得DM,根据相似三角形的判定与性质,可得DE的长,根据二次函数的性质,可得答案;
(3)根据正切函数,可得∠CFO,根据相似三角形的性质,可得GH,BH,根据待定系数法,可得CG的解析式,根据解方程组,可得答案.
(1)由题意,得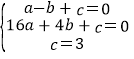 ,
,
解得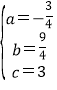 ,
,
抛物线的函数表达式为y=-![]() x2+
x2+![]() x+3;
x+3;
(2)设直线BC的解析是为y=kx+b,
![]() ,
,
解得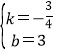 ,
,
∴y=-![]() x+3,
x+3,
设D(a,-![]() a2+
a2+![]() a+3),(0<a<4),过点D作DM⊥x轴交BC于M点,如图1
a+3),(0<a<4),过点D作DM⊥x轴交BC于M点,如图1
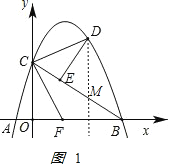 ,
,
M(a,-![]() a+3),
a+3),
DM=(-![]() a2+
a2+![]() a+3)-(-
a+3)-(-![]() a+3)=-
a+3)=-![]() a2+3a,
a2+3a,
∵∠DME=∠OCB,∠DEM=∠BOC,
∴△DEM∽△BOC,
∴![]() ,
,
∵OB=4,OC=3,
∴BC=5,
∴DE=![]() DM
DM
∴DE=-![]() a2+
a2+![]() a=-
a=-![]() (a-2)2+
(a-2)2+![]() ,
,
当a=2时,DE取最大值,最大值是![]() ,
,
(3)假设存在这样的点D,△CDE使得中有一个角与∠CFO相等,
∵点F为AB的中点,
∴OF=![]() ,tan∠CFO=
,tan∠CFO=![]() =2,
=2,
过点B作BG⊥BC,交CD的延长线于G点,过点G作GH⊥x轴,垂足为H,如图2
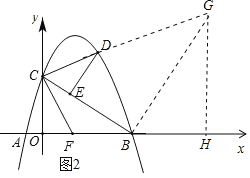 ,
,
①若∠DCE=∠CFO,
∴tan∠DCE=![]() =2,
=2,
∴BG=10,
∵△GBH∽BCO,
∴![]()
∴GH=8,BH=6,
∴G(10,8),
设直线CG的解析式为y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴直线CG的解析式为y=![]() x+3,
x+3,
∴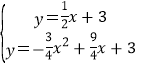 ,
,
解得x=![]() ,或x=0(舍).
,或x=0(舍).
②若∠CDE=∠CFO,
同理可得BG=![]() ,GH=2,BH=
,GH=2,BH=![]() ,
,
∴G(![]() ,2),
,2),
同理可得,直线CG的解析是为y=-![]() x+3,
x+3,
∴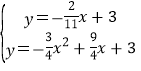 ,
,
解得x=![]() 或x=0(舍),
或x=0(舍),
综上所述,存在点D,使得△CDE中有一个角与∠CFO相等,点D的横坐标为![]() 或
或![]() .
.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案