题目内容
【题目】如图,已知△ABC中,AC=BC=5,AB=5![]() ,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.
,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.

【答案】4.
【解析】
如图作,AM⊥L3于M,BN⊥L3于N.只要证明△ACM≌△CBN(AAS),即可推出AM=CN=3,在Rt△NCB中,利用勾股定理即可解决问题;
解:如图作,AM⊥L3于M,BN⊥L3于N.
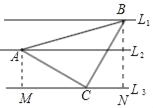
∵AC=BC=5,AB=5![]() ,
,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∵∠AMC=∠BNC=90°,
∴∠ACM+∠BCN=90°,
∵∠BCN+∠CBN=90°,
∴∠ACM=∠CBN,
∴△ACM≌△CBN(AAS),
∴AM=CN=3,
在Rt△NCB中,BN=![]() =4,
=4,
故答案为4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目