题目内容
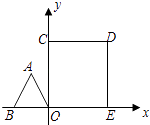
【题目】已知如图，∠AOB：∠BOC＝5：3，OD是∠BOC的平分线，OE是∠AOC的平分线，且∠BOE＝16°，求∠DOE的度数．
【答案】40°.
【解析】
设∠BOC＝3x°，则∠AOB＝5x°，∠AOC＝8x°，再根据角平分线的定义用x表示出∠COE，通过∠BOE＝∠COE﹣∠COB解出值，再根据角的和差关系即可求解．
解：设∠BOC＝3x°，则∠AOB＝5x°，∠AOC＝8x°，
∵OE是∠AOC的平分线，
∴∠COE＝
∠AOC＝4x°．
∵∠BOE＝∠COE﹣∠COB，
∴16°＝5x°﹣4x°，解得x＝16．
∵OD是∠BOC的平分线，
∴∠BOD＝∠BOC＝
＝24°．
∴∠DOE＝∠DOB+∠BOE＝24°+16°＝40°．
故答案为：40°．
练习册系列答案
阅读快车系列答案
相关题目
【题目】学校为了丰富学生课余活动开展了一次“爱我云南，唱我云南”的歌咏比赛，共有18名同学入围，他们的决赛成绩如下表：
成绩（分） | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是（ ）
A.9.70，9.60
B.9.60，9.60
C.9.60，9.70
D.9.65，9.60
