题目内容
【题目】A，B两地被大山阻隔，若要从A地到B地，只能沿着如图所示的公路先从A地到C地，再由C地到B地．现计划开凿隧道A，B两地直线贯通，经测量得：∠CAB=30°，∠CBA=45°，AC=20km，求隧道开通后与隧道开通前相比，从A地到B地的路程将缩短多少？（结果精确到0.1km，参考数据： 
≈1.414， 
≈1.732）
【答案】解：过点C作CD⊥AB与D，
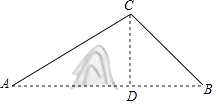
∵AC=20km，∠CAB=30°，
∴CD= 
AC= ×20=10km，
AD=cos∠CABAC=cos30°×20=10 
km，
∵∠CBA=45°，
∴BD=CD=10km，BC= 
CD=10 ≈14.14km
∴AB=AD+BD=10 +10≈27.32km．
则AC+BC﹣AB≈20+14.14﹣27.32≈6.8km．
答：从A地到B地的路程将缩短6.8km．
【解析】解非直角三角形时，若出现特殊角（30°、45°、60°），可过三角形的某一顶点作垂线，使特殊角处于直角三角形中，利用三角函数得出边之间的关系，本题中所求的缩短距离就是求（AC+BC﹣AB）.
练习册系列答案
相关题目
【题目】学校为了丰富学生课余活动开展了一次“爱我云南，唱我云南”的歌咏比赛，共有18名同学入围，他们的决赛成绩如下表：
成绩（分） | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是（ ）
A.9.70，9.60
B.9.60，9.60
C.9.60，9.70
D.9.65，9.60
