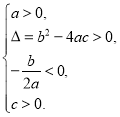题目内容
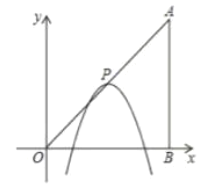
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,抛物线
,抛物线![]() 的顶点
的顶点![]() 在折线
在折线![]() 上运动.
上运动.
(1)当点![]() 在线段
在线段![]() 上运动时,抛物线
上运动时,抛物线![]() 与
与![]() 轴交点坐标为
轴交点坐标为![]() .
.
①用含![]() 的代数式表示
的代数式表示![]() .
.
②求![]() 的取值范围.
的取值范围.
(2)当抛物线与![]() 的边有三个公共点时,试求出点
的边有三个公共点时,试求出点![]() 的坐标.
的坐标.
【答案】(1)①n=m;②![]() ;(2)
;(2)![]() 或
或![]() 或
或![]()
【解析】
(1)①设直线OA的解析式为y=kx,把点(6,6)代入可得k=1,推出y=x.因为y=-(x-m)2+n的顶点P在OA上,推出n=m.②由题意:y=-x2+2mx-m2+m,由抛物线与y轴交点坐标为(0,c),推出c=-m2+m,根据0≤m≤6,利用二次函数的性质即可解决问题;
(2)分三种情形①当抛物线经过点O时,抛物线与△ABO的边有三个公共点,
②当抛物线经过点A时,抛物线与△ABO的边有三个公共点,此时P(6,6);
③当点P在AB上运动,抛物线与OA只有一个公共点时,抛物线与△ABO的边有三个公共点.
解:(1)①设直线![]() 的解析式为
的解析式为![]() ,
,
∵经过![]()
∴![]()
∴![]()
∴![]()
∵![]() 的顶点
的顶点![]() 在
在![]() 上
上
∴![]()
②由题意:![]()
∵抛物线与![]() 轴交点坐标为
轴交点坐标为![]()
∴![]()
∵点![]() 在线段
在线段![]() 上,
上,
∴![]() ,
,![]()
∵![]()
∴当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]() 的取值范围为
的取值范围为![]()
(2)①当抛物线经过点![]() 时,抛物线与
时,抛物线与![]() 的边有三个公共点,
的边有三个公共点,
把![]() 代入抛物线
代入抛物线![]() ,得到
,得到![]() 或0(舍弃),此时
或0(舍弃),此时![]()
②当抛物线经过点![]() 时,抛物线与
时,抛物线与![]() 的边有三个公共点,此时
的边有三个公共点,此时![]() .
.
③当点![]() 在
在![]() 上运动,抛物线与
上运动,抛物线与![]() 只有一个公共点时,抛物线与
只有一个公共点时,抛物线与![]() 的边有三个公共点,
的边有三个公共点,
由 ,消去
,消去![]() 得到
得到![]()
由题意![]() ,∴
,∴![]()
∴![]()
∴![]()
综上所述,满足条件的点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]()

【题目】周老师家的红心猕猴桃深受广大顾客的喜爱,猕猴桃成熟上市后,她记录了15天的销售数量和销售单价,其中销售单价y(元/千克)与时间第x天(x为整数)的数量关系如图所示,日销量P(千克)与时间第x天(x为整数)的部分对应值如下表所示:
时间第x天 | 1 | 3 | 5 | 7 | 10 | 11 | 12 | 15 |
日销量P(千克) | 320 | 360 | 400 | 440 | 500 | 400 | 300 | 0 |
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)从你学过的函数中,选择合适的函数类型刻画P随x的变化规律,请直接写出P与x的函数关系式及自变量x的取值范围;
(3)在这15天中,哪一天销售额达到最大,最大销售额是多少元;
(4)周老师非常热爱公益事业,若在前5天,周老师决定每销售1千克红心猕猴桃就捐献a元给“环保公益项目”,且希望每天的销售额不低于2800元以维持各种开支,求a的最大值.

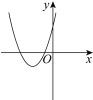
【题目】关于x 的一元二次方程a x2 + bx + c = 0(a>0)有两个不相等且非零的实数根,探究a,b,c满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小华的探究过程:第一步:设一元二次方程ax2 +bx+c = 0(a>0)对应的二次函数为y = ax2 +bx +c(a>0);
第二步:借助二次函数图象,可以得到相应的一元二次方程中a,b,c满足的条件,列表如下:
方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
方程有两个 不相等的负实根 |
|
|
①_______ |
|
|
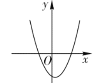
方程有两个 不相等的正实根 | ②__________ | ③____________ |
(1)请帮助小华将上述表格补充完整;
(2)参考小华的做法,解决问题:
若关于x的一元二次方程![]() 有一个负实根和一个正实根,且负实根大于-1,求实数
有一个负实根和一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.