Question

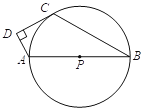
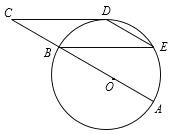
【题目】如图，⊙O的直径AB＝12 cm，C为AB延长线上一点，CD与⊙O相切于点D，过点B作弦BE∥CD，连接DE．

（1）求证：点D为的中点；

（2）若∠C＝∠E，求四边形BCDE的面积．

Answer 1

【答案】（1）见解析 （2）

【解析】

（1）连接OD，由CD与圆O切线，得到OD与CD垂直，根据BE与DC平行，得到OD与BE垂直，进而得到D为弧BE的中点即可；

（2）连接OE，由BE与CD平行，得到一对同位角相等，再由已知角相等，等量代换得到一对内错角相等，进而得到BC与DE平行，即四边形BCDE为平行四边形，求出面积即可．

（1）证明：连接OD交BE于F，

∵CD与⊙O相切于点D，∴OD⊥DC，

∵BE∥CD，∴∠OFB＝∠ODC=90°，

∴OD⊥BE，∴弧BD =弧DE，∴点D为弧BE的中点．

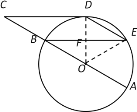
（2）解：连接OE．∵BE∥CD，∴∠C＝∠ABE．

∵∠C＝∠BED，∴∠ABE＝∠BED，∴DE∥CB，

∴四边形BCDE是平行四边形．

∵∠ABE＝∠BED，∴∠AOE＝∠BOD，∴弧AE＝弧BD．

∵弧BD＝弧DE，∴弧BD＝弧DE＝弧AE，

∴∠BOD＝∠DOE＝∠AOE＝60°．∴△DOE为等边三角形．

又∵OD⊥BE，∴DF＝OF＝OD＝3，BF＝EF．

在Rt△OEF中，EF＝＝＝，BE＝．

∴四边形BCDE的面积＝＝＝．