题目内容
【题目】十九大报告中提出“广泛开展全民健身活动,加快推进体育强国建设”.为了响应号召,提升学生训练兴趣,某中学自编“功夫扇”课间操.若设最外侧两根大扇骨形成的角为∠COD,当“功夫扇”完全展开时∠COD=160°.在扇子舞动过程中,扇钉O始终在水平线AB上.
小华是个爱思考的孩子,不但将以上实际问题抽象为数学问题,而且还在抽象出的图中画出了∠BOC 的平分线OE,以便继续探究.
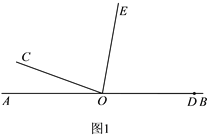
(1)当扇子完全展开且一侧扇骨OD呈水平状态时,如图1所示.请在抽象出的图2中画出∠BOC 的平分线OE,此时∠DOE的度数为 ;

(2)“功夫扇”课间操有一个动作是把扇子由图1旋转到图3所示位置,即将图2中的∠COD绕点O旋转至图4所示位置,其他条件不变,小华尝试用如下两种方案探究了∠AOC和∠DOE度数之间的关系.

方案一:设∠BOE的度数为x.
可得出![]() ,则
,则![]() .
.
![]() ,则
,则![]() .
.
进而可得∠AOC和∠DOE度数之间的关系.
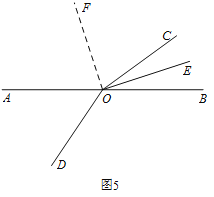
方案二:如图5,过点O作∠AOC的平分线OF.

易得![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() .
.
进而可得∠AOC和∠DOE度数之间的关系.
参考小华的思路可得∠AOC和∠DOE度数之间的关系为 ;
(3)继续将扇子旋转至图6所示位置,即将∠COD绕点O旋转至如图7所示的位置,其他条件不变,请问(2)中结论是否依然成立?说明理由.

【答案】(1)80°;(2)![]() ;(3)不成立
;(3)不成立
【解析】试题分析:(1)根据题意画出角平分线,然后根据角平分线的定义进行求解即可;
(2)结合图形完成题中所给两个方案的过程即可得;
(3)不成立,按(2)中的两个方案进行验证即可得.
试题解析:(1)如图1,
∵OE平分∠COD,∠COD=160°,
∴∠DOE=![]() ∠COD=80°,
∠COD=80°,
故答案为:80°;
(2)方案一:设∠BOE的度数为x,
∵OE平分∠BOC,∴∠BOC=2∠BOE=2x,
∴![]() ,则
,则![]() ,
,
![]() ,则
,则![]() ,
,
∴![]() =
= ![]() ,
,
∴![]() ;
;
方案二:如图5,过点O作∠AOC的平分线OF,
∵OE平分∠BOE,OF平分∠AOC,∴∠COE=![]() ∠BOC,∠COF=
∠BOC,∠COF=![]() ∠AOC,
∠AOC,
∵∠AOC+∠BOC=180°,∴∠COE+∠COF=90°,即![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
故答案为: ![]() ;
;
(3)不成立.
理由如下:
方法一:设∠BOE的度数为x.
可得出![]() ,则
,则![]() .
.
![]() ,则
,则![]() .
.
所以![]() .
.
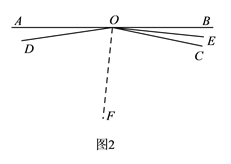
方法二:如图2,过点O作∠AOC的平分线OF.
易得![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() .
.
所以![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案