题目内容
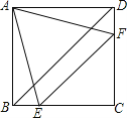
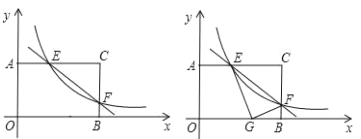
【题目】矩形AOBC中,OB=4,OA=3.分别以OB、OA所在直线为x轴、y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B、C重合).过点F的反比例函数y=![]() (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.
(1)当点F运动到边BC的中点时,点E的坐标为__________;
(2)连接EF,求∠EFC的正切值;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求BG的长度.
【答案】(1)E(2,3);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先确定出点C坐标,进而得出点F坐标,即可求出反比例函数解析式,再根据E点纵坐标为3即可确定E点坐标;
(2)先确定出点F的横坐标,进而表示出点F的坐标,得出CF,同理表示出CE,即可得出结论;
(3)过点E作EH⊥OB于H,先判断出△EHG∽△GBF,根据相似三角形对应边成比例即可求出BG.
解:(1)∵OA=3,OB=4,
∴B(4,0),C(4,3),
∵F是BC的中点,
![]() ,
,
∵F在反比例![]() 函数图象上,
函数图象上,
![]() ,
,
∴反比例函数的解析式为![]() ,
,
∵E点的纵坐标为3,
∴E(2,3);
(2)∵F点的横坐标为4,
![]()
![]() ,
,
∵E的纵坐标为3,
![]()
![]()
在Rt△CEF中,![]() ;
;
(3)如图,由(2)知,![]() ,
,
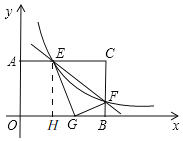
过点E作EH⊥OB于H,
∴EH=OA=3,∠EHG=∠GBF=90°,
∴∠EGH+∠HEG=90°,
由折叠知,![]() ,
,![]() ,∠EGF=∠C=90°,
,∠EGF=∠C=90°,
∴∠EGH+∠BGF=90°,
∴∠HEG=∠BGF,
∵∠EHG=∠GBF=90°,
∴△EHG∽△GBF,
![]() ,
,
![]() ,即
,即![]() .
.

练习册系列答案
相关题目