题目内容
【题目】如图，在
中，
，
，
，将绕点
旋转得到
（
与
，
与
分别是对应顶点），且点，，在同一直线上，以为圆心，
为半径画弧交边
于点
，则
的长为__________．
【答案】
【解析】
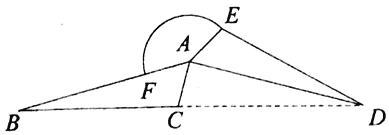
先根据旋转的性质得出∠DAE=∠BAC=60°，AE=AC=3，AB=AD．再由等腰三角形的性质以及三角形内角和定理求出∠BAD=180°-∠ADB-∠B=150°，根据周角的定义得出∠EAF=360°-∠BAD-∠DAE=150°，然后利用弧长计算公式列式计算即可．
解：∵将△ABC绕点A旋转得到△ADE（B与D，C与E分别是对应顶点），
∴∠DAE=∠BAC=60°，AE=AC=3，AB=AD．
∵点B，C，D在同一直线上，AB=AD，
∴∠ADB=∠B=15°，
∴∠BAD=180°-∠ADB-∠B=150°，
∴∠EAF=360°-∠BAD-∠DAE=360°-150°-60°=150°，
∴
的长为：
．
故答案为：
．
【题目】大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商品，此类新型商品在第x天的销售量p件与销售的天数x的关系如下表：
x（天） | 1 | 2 | 3 | … | 50 |
p（件） | 118 | 116 | 114 | … | 20 |
销售单价q（元/件）与x满足：当1≤x＜25时q=x+60；当25≤x≤50时q=40+
．
（1）请分析表格中销售量p与x的关系，求出销售量p与x的函数关系．
（2）求该超市销售该新商品第x天获得的利润y元关于x的函数关系式．
（3）这50天中，该超市第几天获得利润最大？最大利润为多少？
【题目】为了解学生的课外阅读情况，七（1）班针对“你最喜爱的课外阅读书目”进行调查（每名学生必须选一类且只能选一类阅读书目），并根据调查结果列出统计表，绘制成扇形统计图．
男、女生所选类别人数统计表
类别 | 男生（人） | 女生（人） |
文学类 | 12 | 8 |
史学类 |
| 5 |
科学类 | 6 | 5 |
哲学类 | 2 |
|
根据以上信息解决下列问题
（1）
，
；
（2）扇形统计图中“科学类”所对应扇形圆心角度数为 
；
（3）从选哲学类的学生中，随机选取两名学生参加学校团委组织的辩论赛，请用树状图或列表法求出所选取的两名学生都是男生的概率．
