题目内容
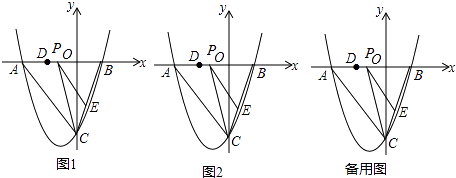
【题目】如图,抛物线y=ax2+bx﹣3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为x=﹣1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合).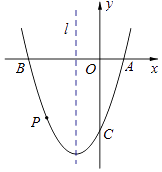
(1)直接写出抛物线的解析式;
(2)小唐探究点P的位置时发现:当动点N在对称轴l上时,存在PB⊥NB,且PB=NB的关系,请求出点P的坐标;
(3)是否存在点P使得四边形PBAC的面积最大?若存在,请求出四边形PBAC面积的最大值;若不存在,请说明理由.
【答案】
(1)
解:∵A(1,0),对称轴l为x=﹣1,
∴B(﹣3,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线的解析式为y=x2+2x﹣3;
(2)
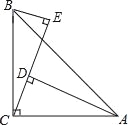
解:如图1,过点P作PM⊥x轴于点M,
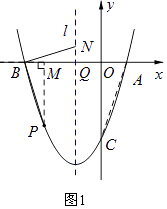
设抛物线对称轴l交x轴于点Q.
∵PB⊥NB,∴∠PBN=90°,
∴∠PBM+∠NBQ=90°.
∵∠PMB=90°,
∴∠PBM+∠BPM=90°.
∴∠BPM=∠NBQ.
又∵∠BMP=∠BNQ=90°,PB=NB,
∴△BPM≌△NBQ.
∴PM=BQ.
∵抛物线y=x2+2x﹣3与x轴交于点A(1,0)和点B,且对称轴为x=﹣1,
∴点B的坐标为(﹣3,0),点Q的坐标为(﹣1,0).∴BQ=2.∴PM=BQ=2.
∵点P是抛物线y=x2+2x﹣3上B、C之间的一个动点,
∴结合图象可知点P的纵坐标为﹣2,
将y=﹣2代入y=x2+2x﹣3,得﹣2=x2+2x﹣3,
解得x1=﹣1﹣ ![]() ,x2=﹣1+
,x2=﹣1+ ![]() (舍去),
(舍去),
∴此时点P的坐标为(﹣1﹣ ![]() ,﹣2)
,﹣2)
(3)
解:存在.
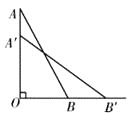
如图2,连接AC.
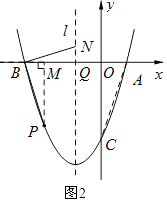
可设点P的坐标为(x,y)(﹣3<x<0),则y=x2+2x﹣3,
∵点A(1,0),∴OA=1.
∵点C是抛物线与y轴的交点,
∴令x=0,得y=﹣3.即点C(0,﹣3).
∴OC=3.
由(2)可知S四边形PBAC=S△BPM+S四边形PMOC+S△AOC
= ![]() BMPM+
BMPM+ ![]() (PM+OC)OM+
(PM+OC)OM+ ![]() OAOC
OAOC
= ![]() (x+3)(﹣y)+
(x+3)(﹣y)+ ![]() (﹣y+3)(﹣x)+
(﹣y+3)(﹣x)+ ![]() ×1×3
×1×3
=﹣ ![]() y﹣
y﹣ ![]() x+
x+ ![]() .
.
将y=x2+2x﹣3代入可得S四边形PBAC=﹣ ![]() (x2+2x﹣3)﹣
(x2+2x﹣3)﹣ ![]() x+
x+ ![]() =﹣
=﹣ ![]() (x+
(x+ ![]() )2+
)2+ ![]() .
.
∵﹣ ![]() <0,﹣3<x<0,
<0,﹣3<x<0,
∴当x=﹣ ![]() 时,S四边形PBAC有最大值
时,S四边形PBAC有最大值 ![]() .此时,y=x2+2x﹣3=﹣
.此时,y=x2+2x﹣3=﹣ ![]() .
.
∴当点P的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )时,四边形PBAC的面积最大,最大值为
)时,四边形PBAC的面积最大,最大值为 ![]() .
.
【解析】(1)由对称轴可求得B点坐标,结合A、B两点坐标,利用待定系数法可求得抛物线解析式;(2)过点P作PM⊥x轴于点M,设抛物线对称轴l交x轴于点Q.可证明△BPM≌△NBQ,则可求得PM=BQ,可求得P点的纵坐标,利用抛物线解析式可求得P点坐标;(3)连接AC,设出P点坐标,则可表示出四边形PBAC的面积,再利用二次函数的性质可求得其最大值.

【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.