题目内容
【题目】已知正方形ABCD和正方形CEFG,连结AF交BC于点O,点P是AF的中点,过点P作PH⊥DG于H,CD=2,CG=1.
(1)如图1,点D、C、G在同一直线上,点E在BC边上,求PH的长;
(2)把正方形CEFG绕着点C逆时针旋转α(0°<α<180°)
①如图2,当点E落在AF上时,求CO的长;
②如图3,当DG=![]() 时,求PH的长.
时,求PH的长.

【答案】(1)PH=![]() ;(2)①CO=
;(2)①CO= ![]() ;②PH=
;②PH=![]() .
.
【解析】试题分析:(1)先判断出四边形APGF是梯形,再判断出PH是梯形的中位线,得到PH=![]() (FG+AD);
(FG+AD);
(2)①先判断出△COE∽△AOB,得到AO是CO的2倍,设出CO,表示出BO,AO,再用勾股定理计算,②先找出辅助线,再判断出△ARD≌△DSC,△CSG≌△GTF,求出AR+FT,最后用梯形中位线即可.
试题解析:(1)PH⊥CD,AD⊥CD,
∴PH∥AD∥FG,
∵点P是AF的中点,
∴PH是梯形APGF的中位线,
∴PH=![]() (FG+AD)=
(FG+AD)=![]() ,
,
(2)①∵∠CEO=∠B=90°,∠COE=∠AOB,
∴△COE∽△AOB,
∴![]() ,
,
∴![]() ,
,
设CO=x,
∴AO=2x,BO=2﹣x,
在△ABO中,根据勾股定理得,4+(2﹣x)2=(2x)2,
∴x=![]() 或x=
或x=![]() (舍),
(舍),
∴CO=x=![]() .
.
②如图3,
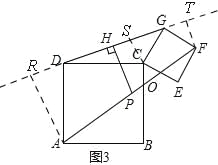
分别过点A,C,F作直线DG的垂线,垂足分别为R,S,T,
∵∠ADR+∠CDS=90°,∠CDS+∠DCS=90°,
∴∠ADR=∠DCS,
∵∠ADR=∠CSD=90°,
∵AD=CD
∴△ARD≌△DSC,
∴AR=DS,
同理:△CSG≌△GTF,
∴SG=FT,
∴AR+FT=DS+SG=DG=![]() ,
,
同(1)的方法得,PH是梯形ARTF的中位线,
∴PH=![]() (AR+FT)=
(AR+FT)=![]() .
.

【题目】某厂生产的RGZ-120型体重秤,最大称重120千克,你在体检时可看到如图(1)所示的显示盘。已知指针顺时针旋转角x(度)与体重y(千克)有如下关系:
x(度) | 0 | 72 | 144 | 216 |
y(千克) | 0 | 25 | 50 | 75 |
(1)根据表格中的数据在平面直角坐标系,图(2)中描出相应的点,顺次连接各点后,你发现这些点在哪一种函数的图象上?合情猜想符合这个图象的函数解析式;
(2)验证这些点的坐标是否满足函数解析式,归纳你的结论(写出自变量x的取值范围);
(3)当指针旋转到158.4度的位置时,显示盘上的体重读数模糊不清,用解析式求出此时的体重。





