题目内容
【题目】已知：关于x的一元二次方程：（m﹣1）x2+（m﹣2）x﹣1=0（m为实数）．
（1）若方程有两个不相等的实数根，求m的取值范围；
（2）若
是此方程的实数根，抛物线y=（m﹣1）x2+（m﹣2）x﹣1与x轴交于A、B，抛物线的顶点为C，求△ABC的面积．
【答案】（1）m的取值范围是m≠0且m≠1；（2）S△ABC=
．
【解析】试题分析：（1）根据方程有两个不相等的实数根可知△＞0，再由一元二次方程的定义得出m≠1，由此可得出结论；
（2）根据
是此方程的实数根可得出m的值，故可得出顶点C的坐标，求出A、B两点的坐标，利用三角形的面积公式即可得出结论．
试题解析：（1）此方程的判别式△=
∵方程有两个不相等的实数根,
∴
.
∵
,
∴
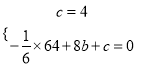的取值范围是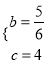
.
（2）
是此方程的实数根，
，
解此方程得： 
.
∴抛物线为
,
化顶点式： 
，
顶点
令
， 得： 
，
.
得
，
.
练习册系列答案
相关题目
