Question

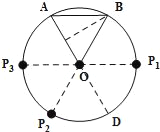
【题目】如图，已知AB是⊙O的弦，半径OA=2，OA和AB的长度是关于x的一元二次方程x2﹣4x+a=0的两个实数根．

（1）求弦AB的长度；

（2）计算S△AOB；

（3）⊙O上一动点P从A点出发，沿逆时针方向运动一周，当S△POA=S△AOB时，求P点所经过的弧长（不考虑点P与点B重合的情形）．

Answer 1

【答案】（1）AB=2；（2）S△AOB=；（3）当S△POA=S△AOB时，P点所经过的弧长分别是、、．

【解析】试题分析：（1）OA和AB的长度是一元二次方程的根，所以利用一元二次方程的根与系数的关系即可求出AB的长度；

（2）作出△AOB的高OC，然后求出OC的长度即可求出面积；

（3）由题意知：两三角形有公共的底边，要面积相等，即高要相等．

试题解析：（1）由题意知：OA和AB的长度是x2﹣4x+a=0的两个实数根，

∴OA+AB=﹣=4，

∵OA=2，

∴AB=2；

（2）过点C作OC⊥AB于点C，

∵OA=AB=OB=2，∴△AOB是等边三角形，∴AC=AB=1，

在Rt△ACO中，由勾股定理可得：OC=，∴S△AOB=AB﹒OC=×2×=；

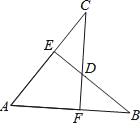
（3）延长AO交⊙O于点D，由于△AOB与△POA有公共边OA，

当S△POA=S△AOB时，∴△AOB与△POA高相等，

由（2）可知：等边△AOB的高为，∴点P到直线OA的距离为，这样点共有3个

①过点B作BP1∥OA交⊙O于点P1，∴∠BOP1=60°，

∴此时点P经过的弧长为： =，

②作点P2，使得P1与P2关于直线OA对称，∴∠P2OD=60°，

∴此时点P经过的弧长为： =，

③作点P3，使得B与P3关于直线OA对称，∴∠P3OP2=60°，

∴此时P经过的弧长为： =，

综上所述：当S△POA=S△AOB时，P点所经过的弧长分别是、、．