题目内容
【题目】如图,平面直角坐标系中,A(1,0)、B(0,2),BA=BC,∠ABC=90°,则点 C 的坐标为___________

【答案】(2,3)
【解析】
过点C作CD⊥y轴于点D,通过角的计算可找出∠OAB=∠DBC,结合∠AOB=∠BDC、AB=BC,即可证出△OAB≌△DBC(AAS),根据全等三角形的性质即可得出BD=AO、DC=OB,再结合点A、B的坐标即可得出DC、OD的长度,进而可得出点C的坐标.
解:过点C作CD⊥y轴于点D,如图所示.
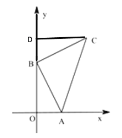
∵∠ABC=90°,∠AOB=90°,
∴∠OAB+∠OBA=90°,∠OBA+∠DBC=90°,
∴∠OAB=∠DBC.
在△OAB和△DBC中,
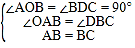 ,
,
∴△OAB≌△DBC(AAS),
∴BD=AO,DC=OB.
∵A(1,0)、B(0,2),
∴BD=AO=1,DC=OB=2,OD=OB+BD=3,
∴点C的坐标为(2,3).
故答案为:(2,3).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】国庆70周年前夕,网店销售 三种规格的手摇小国旗,其部分相关信息如下表:
型号 | 规格(mm) | 批发价(元/面) | 建议零售价(元/面) |
大号 | 45x30 | 2.00 | |
中号 | 28x20 | 1.50 | |
小号 | 22x14 |
已知大号小国旗比中号的批发价贵0.3元,小号小国旗比中号的批发价便宜0.1元某小商品零售商店,第一次用 380元购进了一批大号小国旗,紧接着又用780元购进了第二 批中号小国旗,第二批的数量是第一批的3倍.
(1)求三种型号小国旗的批发价分别是多少元?
(2)该商店很快又购进了第三批小号小国旗1200面.如果三批小国旗全部按网店建议零 售价销售完后,该零售商店获利不少于1980 元,那么小号小国旗的建议零售价至少 为多少元?