题目内容
【题目】已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD,CE相交于点N,则下列五个结论:①AD=BE;②AP=BM;③∠APM=60°;④△CMN是等边三角形;⑤连接CP,则CP平分∠BPD,其中,正确的是_____.(填写序号)

【答案】①③④⑤.
【解析】
①根据△ACD≌△BCE(SAS)即可证明AD=BE;②根据△ACN≌△BCM(ASA)即可证明AN=BM,从而判断AP≠BM;③根据∠CBE+∠CDA=60°即可求出∠APM=60°;④根据△ACN≌△BCM及∠MCN=60°可知△CMN为等边三角形;⑤根据角平分线的性质可知.
①∵△ABC和△CDE都是等边三角形
∴CA=CB,CD=CE,∠ACB=60°,∠DCE=60°
∴∠ACE=60°
∴∠ACD=∠BCE=120°
在△ACD和△BCE中
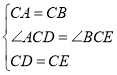
∴△ACD≌△BCE(SAS)
∴AD=BE;
②∵△ACD≌△BCE
∴∠CAD=∠CBE
在△ACN和△BCM中
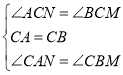
∴△ACN≌△BCM(ASA)
∴AN=BM;
③∵∠CAD+∠CDA=60°
而∠CAD=∠CBE
∴∠CBE+∠CDA=60°
∴∠BPD=120°
∴∠APM=60°;
④∵△ACN≌△BCM
∴CN=BM
而∠MCN=60°
∴△CMN为等边三角形;
⑤过C点作CH⊥BE于H,CQ⊥AD于Q,如图
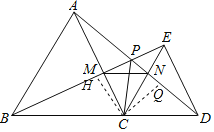
∵△ACD≌△BCE
∴CQ=CH
∴CP平分∠BPD.
故答案为:①③④⑤.

练习册系列答案
相关题目