Question

【题目】如图，已知AB是⊙O的直径，点M在BA的延长线上，MD切⊙O于点D，过点B作BN⊥MD于点C，连接AD并延长，交BN于点N．

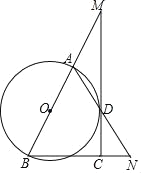
（1）求证：AB=BN；

（2）若MD=4,CD=2.4，求 。

（3）若AM=2，CN=1.2,求⊙O的半径长。

Answer 1

【答案】（1）见解析；（2）；（3）3

【解析】

（1）连接OD，由MD切⊙O于点D，得到OD⊥MD，由于BN⊥MC，得到OD∥BN，得出∠ADO=∠N，根据等腰三角形的性质和等量代换可得结果；（2）利用题目条件证明△ADH≌△NDC，从而得到DH=DC=2.4，MH=4-2.4=1.6，MC=4+2.4=6.4，然后利用平行线分线段成比例定理求得的值；（3）设圆的半径为x，由题目条件证得OD∥AH，然后得到△MAH∽△MOD，根据相似三角形的性质列出比例式求解.

解：（1）连接OD

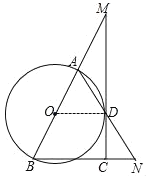
∵MD切⊙O于点D

∴OD⊥MD

又∵BN⊥MD于点C

∴OD∥BN

∴∠ADO=∠N

又∵OD=OA

∴∠OAD=∠ADO

∴∠OAD=∠N

∴AB=BN；

（2）过点A作AH⊥MC

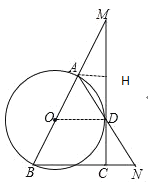
∵OD∥BN

∴

∴OD=DN

又∵AH⊥MC，BN⊥MD

∴AH∥BN

∴∠HAD=∠N

又∵∠ADH=∠NDC

∴△ADH≌△NDC

∴DH=DC=2.4，MH=4-2.4=1.6，MC=4+2.4=6.4

∴

（3）设⊙O的半径为x，

∵MD切⊙O于点D

∴OD⊥MD

又∵AH⊥MC，

∴OD∥AH

∴△MAH∽△MOD

∴

又∵△ADH≌△NDC

∴AH=CN=1.2

∴

得x=3，

经检验x=3是原分式方程的解

即⊙O的半径为3