��Ŀ����
����Ŀ��һ����ѧ�κ���ʦ������һ���κ���ϰ�⣺
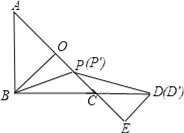
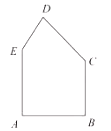
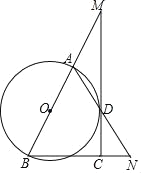
��ͼ����֪��Rt��ABC�У�AB=BC����ABC=90����BO��AC�ڵ�O����P��D�ֱ���AO��BC�ϣ�PB=PD��DE��AC�ڵ�E����֤����BPO�ա�PDE��
����˼·������֤����˼·�������п�ͼ��ʾ��
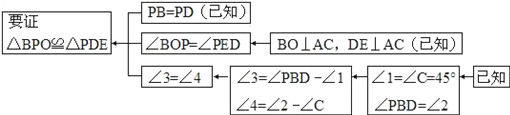
��������˼·����������������⣮
��1����BPƽ����ABO�������������䣮��֤��AP=CD��
��2������P��һ�����㣬��P�˶���OC���е�P��ʱ���������������ĵ�DҲ��֮��ֱ��BC���˶�����D������ֱ��д��CD����AP����������ϵ,��֤���ó��Ĺ�ϵ.
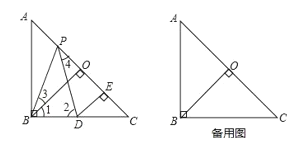
���𰸡���1��֤������������2��CD��=![]() AP�������ɼ�����.
AP�������ɼ�����.
��������
��1���������3����4���������ABP����4�������ABP�ա�CPD�����ɵó��𰸣�
��2����OP��CP��x�����AP��3x��CD��![]() x�����ɵó��𰸣�
x�����ɵó��𰸣�
��1��֤����
��PB��PD��
���2����PBD��
��AB��BC����ABC��90�㣬
���C��45�㣬
��BO��AC��
���1��45�㣬
���1����C��45�㣬
�ߡ�3����PBC��1����4����2��C��
���3����4��
��BPƽ����ABO��
���ABP=��3��
���ABP=��4��
����ABP����CPD��
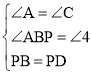
���ABP�ա�CPD��AAS����
��AP=CD��
��2���⣺CD����AP����������ϵ��CD��=![]() AP����
AP����
�����ǣ���OP=PC=x����AO=OC=2x=BO��
��AP=2x+x=3x��
����OBP�ա�EPD����BO=PE��
PE=2x��CE=2x��x=x��
�ߡ�E=90������ECD=��ACB=45����
��DE=x���ɹ��ɶ����ã�CD=![]() x��
x��
��AP=3x��CD=![]() x��
x��
��CD����AP����������ϵ��CD��=![]() AP��
AP��