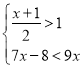题目内容
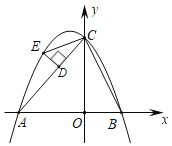
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点,过点P作平行于y轴的直线PM,交线段BC于M,当△PCM是以PM为腰的等腰三角形时,点P的坐标是( )
A.(2,-3)或(![]() +1,—2)B.(2,-3)或(
+1,—2)B.(2,-3)或(![]() ,-1-2
,-1-2![]() )
)
C.(2,-3)或(![]() ,-1-2
,-1-2![]() )D.(2,-3)或(3-
)D.(2,-3)或(3-![]() ,2-4
,2-4![]() )
)
【答案】D
【解析】
根据待定系数法,求得函数解析式,然后求出直线BC的解析式,设设M(n,n-3),P(n,n2-2n-3),分情况讨论,结合勾股定理得方程,从而解方程求得n的值,确定点P的坐标.
解:将B(3,0),C(0,-3)代入函数解析式,得
![]() ,
,
解得![]() ,
,
∴这个二次函数的表达式![]() ;
;
由题意可知:点P在第四象限
设BC的解析式为y=kx+b,
将B(3,0),C(0,-3)的坐标代入函数解析式,得![]() ,
,
解得![]() ,
,
∴BC的解析式为y=x-3,
过点P做PH⊥x轴于点H,与线段BC交于点M,连接PC
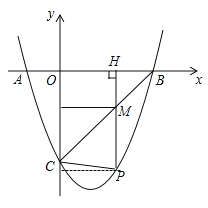
设M(n,n-3),P(n,n2-2n-3),
PM=(n-3)-(n2-2n-3)=-n2+3n=
当PM=PC时,根据勾股定理可得:
![]() ,
,
解得n1=n2=0(不符合题意,舍),n3=2,
n2-2n-3=-3,
∴P(2,-3).
当PM=MC时,根据勾股定理可得:
![]()
解得n1=0(不符合题意,舍),n2=3-![]() ,n3=3+
,n3=3+![]() (不符合题意,舍),
(不符合题意,舍),
n2-2n-3=2-4![]() ,
,
P(3-![]() ,2-4
,2-4![]() )
)
综上所述:P(2,-3)或(3-![]() ,2-4
,2-4![]() ).
).
故选:D

 导学全程练创优训练系列答案
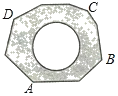
导学全程练创优训练系列答案【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为2米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 20 | 59 | 123 | … |
小石子落在圆外的阴影部分(含外缘)的次数n | 29 | 91 | 176 | … |
(1)当投掷的次数很大时,则m:n的值越来越接近 (结果精确到0.1)
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1);
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留π)
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③