题目内容
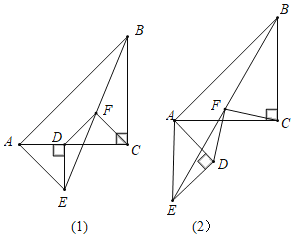
【题目】已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF,CF.
(1)如图1,点D在AC上,请你判断此时线段DF,CF的关系,并证明你的判断;
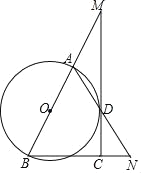
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45度时,若AD=DE=2,AB=6,求此时线段CF的长.
【答案】(1)DF=CF,DF⊥CF,(2)![]() .
.
【解析】
(1)如图1,延长DF交BC于H,由“AAS”可证△DEF≌△HBF,可得DF=FH,DE=BH,可证DC=CH,由等腰直角三角形的性质可得DF=CF,DF⊥CF;
(2)延长DF交BA于点H,连接CH,CD,由“AAS”可证△DEF≌△HBF,可得DF=FH,DE=BH,由“SAS”可证△ADC≌△BHC,可得CH=CD,∠ACD=∠BCH,由由勾股定理和等腰直角三角形的性质可求CF的长.
解:(1)DF=CF,DF⊥CF,
理由如下:如图1,延长DF交BC于H,
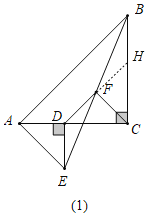
∵点F为BE中点,
∴BF=EF,
∵△ABC和△ADE都是等腰直角三角形,
∴AD=ED,AC=BC,∠ACB=∠ADE=∠CDE=90°,
∴BC∥DE,
∴∠BHF=∠EDF,且BF=EF,∠DFE=∠BFH,
∴△DEF≌△HBF(AAS)
∴DF=FH,DE=BH,
∵AD=ED=BH,AC=BC
∴DC=CH,且DF=FH,∠ACB=90°,
∴CF=DF,CF⊥DF;
(2)如图2,延长DF交BA于点H,连接CH,CD,
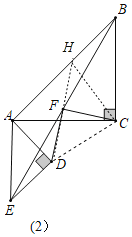
∵△ABC和△ADE是等腰直角三角形,
∴AC=BC,AD=DE.
∴∠AED=∠ABC=45°,
∵由旋转可以得出,∠CAE=∠BAD=90°,
∵AE∥BC,
∴∠AEB=∠CBE,
∴∠DEF=∠HBF.
∵F是BE的中点,
∴EF=BF,且∠DEF=∠HBF,∠EFD=∠BFH,
∴△DEF≌△HBF(AAS),
∴ED=HB=2,DF=FH,
∵AB=6,
∴AH=4
在Rt△HAD中,DH=![]()
∵AD=BH=DE,AC=BC,∠DAC=∠ABC=45°,
∴△ADC≌△BHC(SAS)
∴CH=CD,∠ACD=∠BCH,
∵∠BCH+∠ACH=90°,
∴∠ACD+∠ACH=90°,
∴∠DCH=90°,且CH=CD,DF=FH,
∴CF=DF=FH=![]() .
.

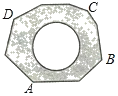
【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为2米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 20 | 59 | 123 | … |
小石子落在圆外的阴影部分(含外缘)的次数n | 29 | 91 | 176 | … |
(1)当投掷的次数很大时,则m:n的值越来越接近 (结果精确到0.1)
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1);
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留π)