Question

【题目】某公司在甲地、乙地分别生产了17台、15台同一种型号的机械设备，现要将这些设备全部运往A、B两市，其中运往A市18台、运往B市14台，从甲地运往A、B两市的费用分别为800元/台和500元/台，从乙地运往A、B两市的费用分别为700元/台和600元/台．设甲地运往A市的设备有x台．
（1）请用x的代数式分别表示甲地运往B市、乙地运往A市、乙地运往B市的设备台数；
（2）求出总运费y（元）与x（台） 的函数关系式，并求出自变量的取值范围；
（3）要使总运费不高于20200元，请你帮助该公司设计调配方案，并写出有哪几种方案，哪种方案总运费最小，最小值是多少？

Answer 1

【答案】
（1）解：甲地运往B市的设备有（17﹣x）台，

乙地运往A市的设备有（18﹣x）台，

乙地运往B市的设备有15﹣（18﹣x）=（x﹣3）台

（2）解：根据题意得：y=800x+500（17﹣x）+700（18﹣x）+600（x﹣3），

即y=200x+19300．

由 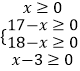，解得3≤x≤17．

∴自变量的取值范围是：x为正整数且3≤x≤17

（3）解：∵要使总运费不高于20200元，

∴200x+19300≤20200，

解得：x≤4.5．（8分）

又∵x为正整数且3≤x≤17，

∴x=3或4．

∴该公司调配方案有两种：

方案一：甲地运往A市3台，运往B市14台，乙地运往A市15台，运往B市0台；

方案二：甲地运往A市4台，运往B市13台，乙地运往A市14台，运往B市1台；

∵在y=200x+19300中，k=200＞0，

∴y随x的增大而增大，

∴当x=3时，总运费最小，最小值是y=200×3+19300=19900（元）．

即甲地运往A市3台，运往B市14台，乙地运往A市15台，运往B市0台总运费最小，最小值是19900元

【解析】（1）根据调配方案，即可解决问题．（2）根据每台的运费即可得出函数关系式；利用不等式求出自变量的取值范围．（3）列出不等式，求整数解，利用一次函数的性质确定最小值．