题目内容
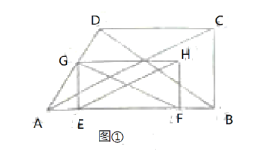
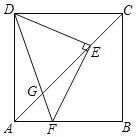
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=12cm,AD=CD=8cm,动点E从点A出发沿AB以每秒1cm的速度向点B运动,动点F从点B出发沿BA以每秒1cm的速度向点A运动,过点E作AB的垂线交折线AD-DC于点G,以EG、EF为邻边作矩形EFHG,设点E、F运动的时间为t(秒),矩形EFHG与四边形ABCD重叠部分的面积为S(cm2).
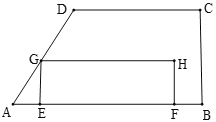
(1)求EG的长(用含t的代数式表示);
(2)当t为何值时,点G与点D重合?
(3)当点G在DC上时,求S(cm2)与t(秒)的函数关系式(S>0);
(4)连接EH、GF、AC、BD,在运动过程中,当这四条线段所在的直线有两条平行时,直接写出t的值.
【答案】(1)GE=![]() t或GE=4
t或GE=4![]() ;(2)t=4;(3)当4≤t<6时,S=-8
;(2)t=4;(3)当4≤t<6时,S=-8![]() t+48
t+48![]() ;当6<t≤8时,S=8
;当6<t≤8时,S=8![]() t-48
t-48![]() ;当8<t≤12,S=
;当8<t≤12,S=![]() ;(4)t=
;(4)t=![]() 或t=3或t=10.
或t=3或t=10.
【解析】
(1)分两种情况讨论:①当点G在AD上时,②当点G在DC上时,分别计算即得.
(2)当点G与点D重合时,可得AE=t,从而可得AG=2t,由AG=AD=8,从而求出t值.
(3)当4≤t<6时,重叠面积是矩形EFHG,FG=4![]() , EF=12-2t,利用矩形的面积公式直接计算即得.当6<t≤8时,重叠面积是矩形EFGH,FG=4
, EF=12-2t,利用矩形的面积公式直接计算即得.当6<t≤8时,重叠面积是矩形EFGH,FG=4![]() ,EF=2t-12,利用矩形的面积公式直接计算即得。 当8<t≤12时,重叠面积是五边形,直接用矩形的面积减去三角形的面积即得。
,EF=2t-12,利用矩形的面积公式直接计算即得。 当8<t≤12时,重叠面积是五边形,直接用矩形的面积减去三角形的面积即得。
(3)分三种情况讨论,如图①当EH∥AC时,可得等式![]() , 解出t即可. 如图②当GF∥BD时,
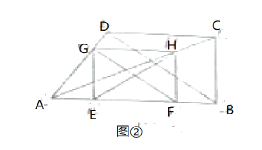
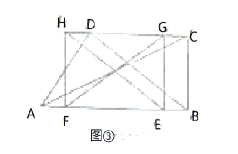
, 解出t即可. 如图②当GF∥BD时,![]() ,解出t即可.如图③当EH∥BD时,可得12-t=t-8,解出t即可.
,解出t即可.如图③当EH∥BD时,可得12-t=t-8,解出t即可.
(1)当点G在AD上时,GE=![]() t;当点G在DC上时,GE=4
t;当点G在DC上时,GE=4![]() ;
;
(2)当点G与D重合时,2t=8,t=4;
(3)解:当4≤t<6时,S=4![]() (12-2t)=-8
(12-2t)=-8![]() t+48
t+48![]() ;
;
当6<t≤8时,S=4![]() (2t-12)=8
(2t-12)=8![]() t-48
t-48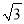 ;
;
当8<t≤12,S=(8![]() t-48
t-48![]() )-
)-![]() ×
×![]() (t-8)2=
(t-8)2= ![]() .
.
(4)解:如图①,当 ![]() 时,t=
时,t=![]() ;
;
如图②,当![]() 时,t=3;
时,t=3;
如图③,当12-t=t-8时,t=10.