题目内容
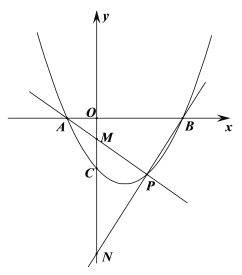
【题目】己知抛物线y=ax2+bx-3a(a>0)与x轴交于A(-1,0)、B两点,与y轴交于点C.
(1)求点B的坐标;
(2)P是第四象限内抛物线上的一个动点.
①若∠APB=90°,且a<3,求点P纵坐标的取值范围;
②直线PA、PB分别交y轴于点M、N求证:![]() 为定值.
为定值.
【答案】(1) B(3,0);(2) ①-2≤n<-![]() ,②
,②![]() =
=![]()
【解析】
(1)把A(-1,0)代入抛物线的解析式,可得a、b的关系,代入取y=0,解方程可得B点坐标.
(2)因为P是第四象限内抛物线上的一个动点.可设设P(m,n), 且m >0, n <0,
①把P(m,n)代入函数解析式,得m、n之间的关系,根据勾股定理列出算式,求出m、n的关系,综合可得到n与a的关系,结合抛物线的顶点坐标及n的取值范围即可确定n的取值范围.
②用待定系数法求直线AP、BP解析式,取x=0求出C、M、N的坐标,表示出CM、CN的长,代入计算即可.
(1)抛物线过A(-1,0)
∴0=a-b-3a,b=-2a,
令y=0,则ax2-2ax-3a=0
a(x2-2x-3)=0, 且a>0
∴B(3,0)
(2)设P(m,n), 且m >0, n <0,则n=am2-2am-3a=a(m2-2m-3).
①AP2=n2+ (m+1)2, BP2=n2+ (3-m)2, AB2=16.
∵∠APB=90°,
∴AP2 +BP2= AB2,即:n2+ (m+1)2+n2+ (3-m)2 =16.
整理后:n2=-m2+2m+3
∴n2=-![]() ,且n <0,
,且n <0,
∴n=-![]() <0
<0
又抛物线顶点(-1,4 a)
∴4a≤-![]() <0,a≥
<0,a≥![]()
又∵a<3
∴![]() ≤a<3
≤a<3
∵-1<0,∴当![]() ≤a<3时,n随a的增大而增大,
≤a<3时,n随a的增大而增大,
∴-2≤n<-![]()
②将x=0代入y=ax2+bx-3a得:y=-3a
∴C(0,-3a)
直线AP过点A(-1,0)、P(m,n)两点,其解析式为:
y=a (m-3)x+ a (m-3),M(0, am-3a)
直线BP过点B(3,0)、P(m,n)两点,其解析式为:
y=a (m+1)x-3a (m+1),N(0, -3am-3a)
∴CM=|-3a-(am-3a)|=| am |
CN=|-3a-(-3am-3a)|=|3am |
∴![]() =
=![]()

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案