题目内容
【题目】阅读下列两则材料,回答问题:
材料一:因为![]() 所以我们将
所以我们将![]() 与
与![]() 称为一対“有理化因式”,有时我们可以通过构造“有理化因式”求值
称为一対“有理化因式”,有时我们可以通过构造“有理化因式”求值
例如:已知![]() ,求
,求![]() 的值
的值
解:![]() ,∵
,∵![]()
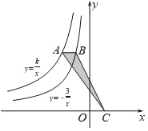
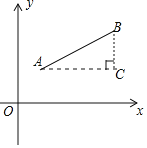
材料二:如图,点A(x1,y1),点B(x2,y2),所以AB为斜边作Rt△ABC,则C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,所以AB=![]() ,反之,可将代数式
,反之,可将代数式![]() 的值看作点(x1,y1)到点(x2,y2)的距离.例如
的值看作点(x1,y1)到点(x2,y2)的距离.例如![]() =
=![]() ,所以可将代数式
,所以可将代数式![]() 的值看作点(x,y)到点(1,﹣1)的距离;
的值看作点(x,y)到点(1,﹣1)的距离;
(1)利用材料一,解关于x的方程:![]() ,其中x≤2;
,其中x≤2;
(2)利用材料二,求代数式![]() 的最小值,并求出此时y与x的函数关系式,写出x的取值范围.
的最小值,并求出此时y与x的函数关系式,写出x的取值范围.
【答案】(1)x=﹣2;(2)y=x+5(﹣3≤x≤1).
【解析】
(1)根据材料一类比计算![]() 的值,利用换元法解方程,可得结论;
的值,利用换元法解方程,可得结论;
(2)把根式下的式子转化成平方+平方的形式,转化成点到点的距离问题,根据两点之间距离最短,所以当三个点共线时距离最短,可以求出最小值和函数关系式.
解:(1)![]() ,
,
![]() ,
,
![]() ;
;
设![]() ,
,
则![]() ,解得:
,解得:![]() ,
,
∴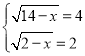 ,
,
∵x≤2,
解得:x=﹣2;
(2)![]() ,
,
![]() ,
,
![]()
![]() ,
,
所以可将![]() 看作点(x,y)到点(1,6)的距离;
看作点(x,y)到点(1,6)的距离;
可将![]() 看作点(x,y)到点(﹣3,2)的距离;
看作点(x,y)到点(﹣3,2)的距离;
∴当代数式![]() 取最小值,
取最小值,
即点(x,y)与点(1,6),(﹣3,2)在同一条直线上,并且点(x,y)位于点(1,6)、(﹣3,2)的中间,
∴![]() 的最小值=
的最小值=![]() ,且﹣3≤x≤1,
,且﹣3≤x≤1,
设过(x,y),(1,6),(﹣3,2)的直线解析式为:y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴y=x+5(﹣3≤x≤1).

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】我市某中学学生会在开展“厉行勤俭节约,反对铺张浪费”的主题教育活动中,在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果,绘制了如下统计表:根据所给信息,回答下列问题:
选项 | 频数 | 频率 |
A | 36 | m |
B | n | 0.2 |
C | 6 | 0.1 |
D | 6 | 0.1 |
(1)统计表中:m=______;n=______.
(2)该中学有1800名学生晚饭在校就餐,根据调查结果,估计当天晚饭有多少人能够把饭和菜全部吃完?
(3)为了对同学们浪费的行为进行纠正,校学生会从饭和菜都有剩的甲、乙、丙、丁四名同学中任取2位同学进行批评教育,请用列表法或树状图法求恰好抽到甲和丁的概率.