题目内容
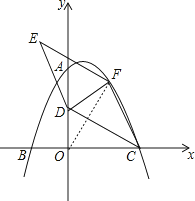
【题目】如图,在平面直角坐标系中,二次函数y=﹣ ![]() x2+bx+c的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
x2+bx+c的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
【答案】
(1)
解:把A(0,8),B(﹣4,0)代入y=﹣ ![]() x2+bx+c得
x2+bx+c得 ![]() ,解得
,解得 ![]() ,
,
所以抛物线的解析式为y=﹣ ![]() x2+x+8;
x2+x+8;
当y=0时,﹣ ![]() x2+x+8=0,解得x1=﹣4,x2=8,
x2+x+8=0,解得x1=﹣4,x2=8,
所以C点坐标为(8,0)
(2)
解:①连结OF,如图,
设F(t,﹣ ![]() t2+t+8),
t2+t+8),
∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,
∴S△CDF=S△ODF+S△OCF﹣S△OCD= ![]() 4t+
4t+ ![]() 8(﹣
8(﹣ ![]() t2+t+8)﹣
t2+t+8)﹣ ![]() 48
48
=﹣t2+6t+16
=﹣(t﹣3)2+25,
当t=3时,△CDF的面积有最大值,最大值为25,
∵四边形CDEF为平行四边形,
∴S的最大值为50;
②∵四边形CDEF为平行四边形,
∴CD∥EF,CD=EF,
∵点C向左平移8个单位,再向上平移4个单位得到点D,
∴点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,﹣ ![]() t2+t+12),
t2+t+12),
∵E(t﹣8,﹣ ![]() t2+t+12)在抛物线上,
t2+t+12)在抛物线上,
∴﹣ ![]() (t﹣8)2+t﹣8+8=﹣
(t﹣8)2+t﹣8+8=﹣ ![]() t2+t+12,解得t=7,
t2+t+12,解得t=7,
当t=7时,S△CDF=﹣(7﹣3)2+25=9,
∴此时S=2S△CDF=18.
【解析】(1)把A点和B点坐标代入y=﹣ ![]() x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标(2)①连结OF,如图,设F(t,﹣
x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标(2)①连结OF,如图,设F(t,﹣ ![]() t2+t+8),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF , 利用三角形面积公式得到S△CDF=﹣t2+6t+16,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值; ②由于四边形CDEF为平行四边形,则CD∥EF,CD=EF,利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,﹣
t2+t+8),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF , 利用三角形面积公式得到S△CDF=﹣t2+6t+16,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值; ②由于四边形CDEF为平行四边形,则CD∥EF,CD=EF,利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,﹣ ![]() t2+t+12),然后把E(t﹣8,﹣
t2+t+12),然后把E(t﹣8,﹣ ![]() t2+t+12)代入抛线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求二次函数解析式;理解坐标与图形性质,掌握点平移的坐标规律.
t2+t+12)代入抛线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求二次函数解析式;理解坐标与图形性质,掌握点平移的坐标规律.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数 | 质量等级 | 天数(天) |
0﹣50 | 优 | m |
51﹣100 | 良 | 44 |
101﹣150 | 轻度污染 | n |
151﹣200 | 中度污染 | 4 |
201﹣300 | 重度污染 | 2 |
300以上 | 严重污染 | 2 |

(1)统计表中m= , n= . 扇形统计图中,空气质量等级为“良”的天数占%;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天?
(3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因,据此,请你提出一条合理化建议.





