题目内容
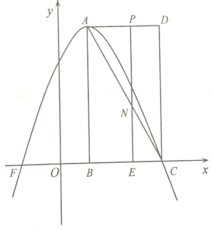
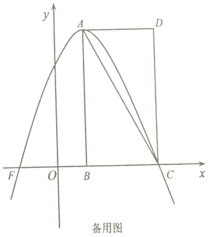
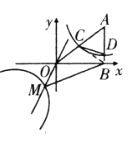
【题目】如图,在平面直角坐标系中,![]() 点的坐标为
点的坐标为![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象的一支经过
的图象的一支经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() .
.
(1)求该反比例函数的表达式;
(2)若函数![]() 与
与![]() 的图象的另一支交于点
的图象的另一支交于点![]() ,求三角形
,求三角形![]() 与四边形
与四边形![]() 的面积比.
的面积比.
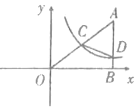
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据![]() 求出OA的长度,再利用勾股定理求出AB的长度,得出点C的坐标,将点C代入函数解析式计算即可得出答案;
求出OA的长度,再利用勾股定理求出AB的长度,得出点C的坐标,将点C代入函数解析式计算即可得出答案;
(2)联立一次函数和反比例函数的解析式求出点M的坐标,设![]() ,代入反比例函数求出点D的坐标即可得出△MOB的面积,四边形OCDB的面积等于△OBC和△BCD面积之和,作比即可得出答案.
,代入反比例函数求出点D的坐标即可得出△MOB的面积,四边形OCDB的面积等于△OBC和△BCD面积之和,作比即可得出答案.
解:(1)∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵点![]() 在反比例函数
在反比例函数![]() 图象上,把
图象上,把![]() 代入
代入![]() 中
中
∴![]() ,故反比例函数表达式为:
,故反比例函数表达式为:![]() ;
;
(2)将![]() 与
与![]() 联立方程组,得
联立方程组,得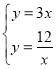 ,
,
∴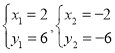 ,∴
,∴![]() ,
,
∵点![]() 在
在![]() 上,
上,![]() 轴,设
轴,设![]() ,代入
,代入![]() 中,∴
中,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
连接![]() ,∵
,∵![]() ,
,
![]() ,
,
∴![]()

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目