题目内容
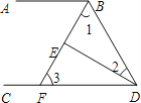
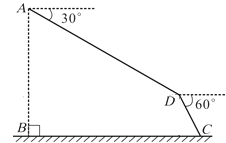
【题目】2017年9月8日—10日,第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行,来自全球11个国家的16名选手参加了激烈的角逐.如图,某选手从离水平地面1000米高的A点出发(AB=1000米),沿俯角为![]() 的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为
的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为![]() 的方向降落到地面上的C点,求该选手飞行的水平距离
的方向降落到地面上的C点,求该选手飞行的水平距离![]() .
.

【答案】![]()
【解析】如图,作DE⊥AB于E,DF⊥BC于F,根据题意得到∠ADE=30°,∠CDF=30°,利用含30度的直角三角形三边的关系计算出AE=![]() AD=700,DE=
AD=700,DE=![]() AE=700
AE=700![]() ,则BE=300,所以DF=300,BF=700
,则BE=300,所以DF=300,BF=700![]() ,再在Rt△CDF中计算出CF,然后计算BF和CF的和即可.
,再在Rt△CDF中计算出CF,然后计算BF和CF的和即可.
如图,作DE⊥AB于E,DF⊥BC于F,∠ADE=30°,∠CDF=30°,
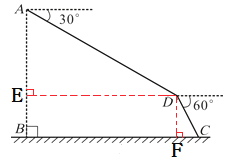
在Rt△ADE中,AE=![]() AD=
AD=![]() ×1400=700,
×1400=700,
DE=![]() AE=700
AE=700![]() ,
,
∴BE=AB-AE=1000-700=300,
∴DF=300,BF=700![]() ,
,
在Rt△CDF中,CF=![]() DF=
DF=![]() ×300=100
×300=100![]() ,
,
∴BC=700![]() +100
+100![]() =800
=800![]() .
.
答:选手飞行的水平距离BC为800![]() m.
m.

练习册系列答案
相关题目