题目内容
【题目】在平行四边形ABCD中，AD=13，
BAD和ADC的角平分线分别交BC于E，F，且EF=6，则平行四边形的周长是____________________
【答案】45或33.
【解析】
需要分两种情况进行讨论.由于平行四边形的两组对边互相平行，又AE平分∠BAD，由此可以推出所以∠BAE=∠DAE，则BE=AB；同理可得，CF=CD=5．而AB+CD=BE+CF=BC+FE=13+6=19，或 AB+CD=BE+CF=BC-FE=13-6=7由此可以求周长．
解：分两种情况，（1）如图，当AE、DF相交时：
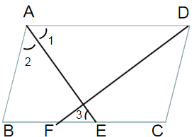
∵AE平分∠BAD，
∴∠1=∠2
∵平行四边形ABCD中，AD∥BC,BC=AD=13，EF=6
∴∠1=∠3
∴∠2=∠3
∴AB=BE
同理CD=CF
∴AB+CD=BE+CF=BC+FE=13+6=19
∴平行四边形ABCD的周长= AB+CD+ BC+AD=19+13×2=45；
（二）当AE、DF不相交时：
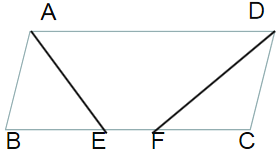
由角平分线和平行线，同（1）方法可得AB=BE，CD=CF
∴AB+CD=BE+CF=BC-FE=13-6=7
∴平行四边形ABCD的周长= AB+CD+ BC+AD=7+13×2=33；
故答案为：45或33.
练习册系列答案
相关题目
【题目】父亲告诉小明：“距离地面越高，温度越低”，并给小明出示了下面的表格：
距离地面高度（千米） | 0 | 1 | 2 | 3 | 4 | 5 |
温度（℃） | 20 | 14 | 8 | 2 | -4 | -10 |
根据表中，父亲还给小明出了下面几个问题，你和小明一起回答．
（1）表中自变量是________；因变量是_________；在地面上（即
时）时，温度是_________℃；
（2）如果用
表示距离地面的高度，用
表示温度，则满足与关系的式子为_____________；
（3）计算出距离地面6千米的高空温度是多少？
