题目内容
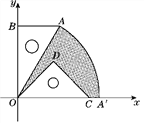
【题目】如图,平行四边形ABCD的边AB在x轴上,点C的坐标为(﹣5,4),点D在y轴的正半轴上,经过点A的直线y=![]() x﹣1与y轴交于点E,将直线AE沿y轴向上平移n(n>0)个单位长度后,得到直线l,直线l经过点C时停止平移.
x﹣1与y轴交于点E,将直线AE沿y轴向上平移n(n>0)个单位长度后,得到直线l,直线l经过点C时停止平移.
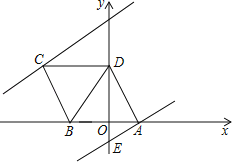
(1)点A的坐标为 ,点B的坐标为 ;
(2)若直线l交y轴于点F,连接CF,设△CDF的面积为S(这里规定:线段是面积为0的三角形),求S与n之间的函数关系式,并写出n的取值范围;
(3)易知AE⊥AD于点A,若直线l交折线AD﹣DC于点P,当△AEP为直角三角形时,请直接写出n的取值范围.
【答案】(1)A(2,0),B(-3,0);(2)当0≤n≤5时,S=10-2n;当5<n≤![]() 时,S=2n-10;(3)n=
时,S=2n-10;(3)n=![]() 或0≤n≤5.
或0≤n≤5.
【解析】
(1)令y=0,则![]() x-1=0,求A(2,0),由平行四边形的性质可知AB=5,则B(-3,0);
x-1=0,求A(2,0),由平行四边形的性质可知AB=5,则B(-3,0);
(2)易求E(0,-1),当l到达C点时的解析式为y=![]() x+
x+![]() ,当0≤n≤5时,S=
,当0≤n≤5时,S=![]() ×4×(5-n)=10-2n;当5<n≤
×4×(5-n)=10-2n;当5<n≤![]() 时,S=
时,S=![]() ×4×(n-5)=2n-10;
×4×(n-5)=2n-10;
(3)由点可以得到AD⊥AE;当P在AD上时,△AEP为直角三角形,0≤n≤5;当P在CD上时,△AEP为直角三角形,则PE⊥AE,设P(m,4),可得![]() =-2,求出P(-
=-2,求出P(-![]() ,4),此时l的解析式为y=
,4),此时l的解析式为y=![]() x+
x+![]() ,则n=
,则n=![]() .
.
(1)令y=0,则![]() x-1=0,x=2,
x-1=0,x=2,
∴A(2,0),
∵C的坐标为(-5,4),四边形ABCD是平行四边形,
∴AB=CD=5,
∴OB=AB-OA=3,∴B(-3,0);
(2)当x=0时,y=![]() x﹣1=-1,所以E(0,-1),
x﹣1=-1,所以E(0,-1),
∵直线AE沿y轴向上平移得到l,当l到达C点时的解析式为y=![]() x+
x+![]() ,
,
此时l与y轴的交点为(0,![]() ),
),
当0≤n≤5时,S=![]() ×4×(5-n)=10-2n;
×4×(5-n)=10-2n;
当5<n≤![]() 时,S=
时,S=![]() ×4×(n-5)=2n-10;
×4×(n-5)=2n-10;
(3)∵D(0,4),A(2,0),E(0,-1),
∴AD=2![]() ,AE=
,AE=![]() ,ED=5,
,ED=5,
∴AD2+AE2=ED2,
∴AD⊥AE,
当P在AD上时,△AEP为直角三角形,
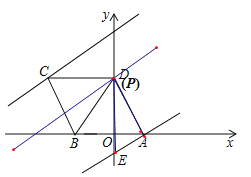
∴0≤n≤5;
当P在CD上时,△AEP为直角三角形,
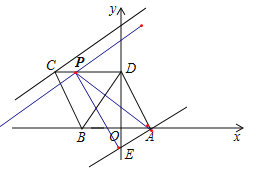
则PE⊥AE,
设P(m,4),
∴![]() =-2,
=-2,
∴m=-![]() ,
,
∴P(-![]() ,4),
,4),
∴此时l的解析式为y=![]() x+
x+![]() ,
,
∴n=![]() ;
;
综上所述:当△AEP为直角三角形时,n=![]() 或0≤n≤5.
或0≤n≤5.

【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:

(1)将下面的表格补充完整:
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | 45° |
|
| … |
|
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.