题目内容
【题目】在如图的网格中,小正方形的边长都是1,利用所学知识两种解法求四边形ABCD的面积,写出完整求解过程.
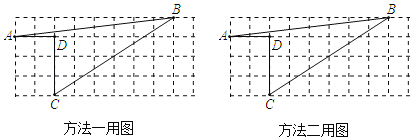
【答案】方法一:见解析;方法二:见解析.
【解析】
方法一,把不规则的四边形ABCD补成规则图形,常规做法是过A、B、C构造以网格线为边长的矩形,用矩形面积减去两个小直角三角形和一个矩形的面积和即得到四边形ABCD的面积.
方法二,通过连接AC把不规则的四边形ABCD补成△ABC,则四边形面积为△ABC面积减去直角△ACD面积.计算得到AB2=65,BC2=52,AC2=13,满足勾股定理逆定理,即△ABC为直角三角形且∠ACB=90°,易求其面积.
方法一:如图,构造矩形GEFB,

∴S△GAB=![]() GAGB=
GAGB=![]() ×1×8=4,
×1×8=4,
S矩形AECD=AEEC=3×2=6,
S△BCF=![]() CFBF=
CFBF=![]() ×6×4=12,
×6×4=12,
S矩形GEFB=GEEF=4×8=32,
∴S四边形ABCD=S矩形GEFB﹣S△GAB﹣S矩形AECD﹣S△BCF =32﹣4﹣6﹣12=10;
方法二:连接AC,得Rt△ADC,

由图形及勾股定理得:AC2=32+22=13,BC2=62+42=52,AB2=82+12=65,
∴AC2+BC2=AB2,
∴△ACB为直角三角形且∠ACB=90°,
∴S△ACB=![]() ACBC=
ACBC=![]() ,
,
S△ADC=![]() ADCD=
ADCD=![]() ×2×3=3,
×2×3=3,
∴S四边形ABCD=S△ACB﹣S△ADC=13﹣3=10.

【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
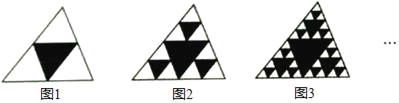
(1)填写下表:
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn