ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈ“Ο«≥ΘΦϊΒΡ≥¥≤ΥΙχΚΆΙχΗ«ΕΦ «≈ΉΈοœΏΟφΘ§Ψ≠ΙΐΙχ–ΡΚΆΗ«–ΡΒΡΉίΕœΟφ «ΝΫΕΥ≈ΉΈοœΏΉιΚœΕχ≥…ΒΡΖβ±’ΆΦ–ΈΘ§≤ΜΖΝΦρ≥ΤΈΣΓΑΙχœΏΓ±Θ§ΙχΩΎ÷±ΨΕΈΣ![]() Θ§Ιχ…ν
Θ§Ιχ…ν![]() Θ§ΙχΗ«ΗΏ
Θ§ΙχΗ«ΗΏ![]() Θ®ΙχΩΎ÷±ΨΕ”κΙχΗ«÷±ΨΕ ”ΈΣœύΆ§Θ©Θ§Ϋ®ΝΔ÷±Ϋ«Ήχ±ξœΒ»γΆΦΔΌΥυ ΨΘ®ΆΦΔΎ «±Η”ΟΆΦΘ©Θ§»γΙϊΑ―ΙχΉίΕœΟφΒΡ≈ΉΈοœΏΦ«ΈΣ
Θ®ΙχΩΎ÷±ΨΕ”κΙχΗ«÷±ΨΕ ”ΈΣœύΆ§Θ©Θ§Ϋ®ΝΔ÷±Ϋ«Ήχ±ξœΒ»γΆΦΔΌΥυ ΨΘ®ΆΦΔΎ «±Η”ΟΆΦΘ©Θ§»γΙϊΑ―ΙχΉίΕœΟφΒΡ≈ΉΈοœΏΦ«ΈΣ![]() Θ§Α―ΙχΗ«ΉίΕœΟφΒΡ≈ΉΈοœΏΦ«ΈΣ
Θ§Α―ΙχΗ«ΉίΕœΟφΒΡ≈ΉΈοœΏΦ«ΈΣ![]() Θ°
Θ°
![]() «σ
«σ![]() ΚΆ
ΚΆ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
![]() »γΙϊ≥¥≤ΥΙχ ±ΒΡΥ°ΈΜΗΏΕ» «
»γΙϊ≥¥≤ΥΙχ ±ΒΡΥ°ΈΜΗΏΕ» «![]() Θ§«σ¥Υ ±Υ°ΟφΒΡ÷±ΨΕΘΜ
Θ§«σ¥Υ ±Υ°ΟφΒΡ÷±ΨΕΘΜ
![]() »γΙϊΫΪ“ΜΗωΒΉΟφ÷±ΨΕΈΣ
»γΙϊΫΪ“ΜΗωΒΉΟφ÷±ΨΕΈΣ![]() Θ§ΗΏΕ»ΈΣ
Θ§ΗΏΕ»ΈΣ![]() ΒΡ‘≤÷υ–ΈΤςΟσΖ≈»κ≥¥≤ΥΙχΡΎ’τ ≥ΈοΘ§ΙχΗ«ΡήΖώ’ΐ≥ΘΗ«…œΘΩ«κΥΒΟςάμ”…Θ°
ΒΡ‘≤÷υ–ΈΤςΟσΖ≈»κ≥¥≤ΥΙχΡΎ’τ ≥ΈοΘ§ΙχΗ«ΡήΖώ’ΐ≥ΘΗ«…œΘΩ«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ![]()
![]() ΘΜ
ΘΜ![]() Θ°
Θ°![]() ¥Υ ±Υ°ΟφΒΡ÷±ΨΕΈΣ
¥Υ ±Υ°ΟφΒΡ÷±ΨΕΈΣ![]() Θ°
Θ°![]() ΙχΗ«Ρή’ΐ≥ΘΗ«…œΘ§άμ”…ΦϊΫβΈω.
ΙχΗ«Ρή’ΐ≥ΘΗ«…œΘ§άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
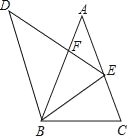
Θ®1Θ©“―÷ΣAΓΔBΓΔCΓΔDΥΡΒψΉχ±ξΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…»ΖΕ®ΝΫΚ· ΐΒΡΫβΈω ΫΘΜ
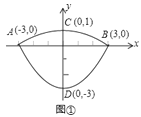
Θ®2Θ©≥¥≤ΥΙχάοΒΡΥ°ΈΜΗΏΕ»ΈΣ1dmΦ¥y=-2Θ§Ν–ΖΫ≥Χ«σΒΟxΒΡ÷ΒΦ¥Ω…ΒΟ¥πΑΗΘΜ
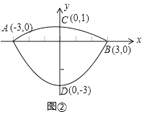
Θ®3Θ©ΒΉΟφ÷±ΨΕΈΣ3dmΓΔΗΏΕ»ΈΣ3dm‘≤÷υ–ΈΤςΟσΡήΖώΖ≈»κΙχΡΎΘ§–η≈–ΕœΒ±![]() ±Θ§C1ΚΆC2÷–ΒΡy÷ΒΒΡ≤ν”κ3±»Ϋœ¥σ–ΓΘ§¥”ΕχΩ…ΒΟ¥πΑΗΘ°
±Θ§C1ΚΆC2÷–ΒΡy÷ΒΒΡ≤ν”κ3±»Ϋœ¥σ–ΓΘ§¥”ΕχΩ…ΒΟ¥πΑΗΘ°
![]() ”…”Ύ≈ΉΈοœΏ
”…”Ύ≈ΉΈοœΏ![]() ΓΔ
ΓΔ![]() ΕΦΙΐΒψ
ΕΦΙΐΒψ![]() ΓΔ
ΓΔ![]() Θ§Ω……ηΥϋΟ«ΒΡΫβΈω ΫΈΣΘΚ
Θ§Ω……ηΥϋΟ«ΒΡΫβΈω ΫΈΣΘΚ![]() ΘΜ
ΘΜ
≈ΉΈοœΏ![]() ΜΙΨ≠Ιΐ
ΜΙΨ≠Ιΐ![]() Θ§
Θ§
‘ρ”–ΘΚ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]()
Φ¥ΘΚ≈ΉΈοœΏ![]() ΘΜ
ΘΜ
≈ΉΈοœΏ![]() ΜΙΨ≠Ιΐ
ΜΙΨ≠Ιΐ![]() Θ§
Θ§
‘ρ”–ΘΚ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]()
Φ¥ΘΚ≈ΉΈοœΏ![]() Θ°
Θ°
![]() Β±≥¥≤ΥΙχάοΒΡΥ°ΈΜΗΏΕ»ΈΣ
Β±≥¥≤ΥΙχάοΒΡΥ°ΈΜΗΏΕ»ΈΣ![]() ±Θ§
±Θ§![]() Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ¥Υ ±Υ°ΟφΒΡ÷±ΨΕΈΣ![]() Θ°
Θ°
![]() ΙχΗ«Ρή’ΐ≥ΘΗ«…œΘ§άμ”…»γœ¬ΘΚ
ΙχΗ«Ρή’ΐ≥ΘΗ«…œΘ§άμ”…»γœ¬ΘΚ
Β±![]() ±Θ§≈ΉΈοœΏ
±Θ§≈ΉΈοœΏ![]() Θ§≈ΉΈοœΏ
Θ§≈ΉΈοœΏ![]() Θ§
Θ§
Εχ![]() Θ§
Θ§
ΓύΙχΗ«Ρή’ΐ≥ΘΗ«…œΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ