题目内容
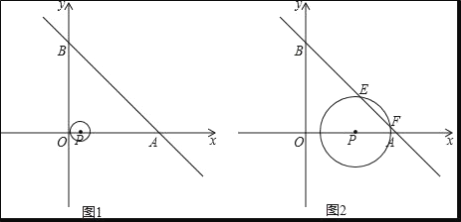
【题目】如图1,一次函数y=﹣x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的⊙P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时⊙P的半径以每秒增加1个单位的速度不断变大,设运动时间为t(s)
(1)点A的坐标为 ,点B的坐标为 ,∠OAB= °;
(2)在运动过程中,点P的坐标为 ,⊙P的半径为 (用含t的代数式表示);
(3)当⊙P与直线AB相交于点E、F时
①如图2,求t=![]() 时,弦EF的长;
时,弦EF的长;
②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).
【答案】(1)(10,0),(0,10),45°.(2)(1+2t,0),1+t.(3)![]() .
.
【解析】试题分析:(1)利用待定系数法求出点A、B的坐标,即可解决问题.
(2)根据题意可得P(1+2t,0),⊙O半径为1+t.
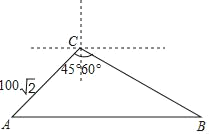
(3)①如图1中,作PK⊥AB于K,连接PE.在Rt△APK中,由∠PKA=90°,∠PAK=45°,PA=4,推出PK=![]() PA=2
PA=2![]() ,在Rt△PEK中,根据EK=
,在Rt△PEK中,根据EK=![]() 计算即可.
计算即可.
②分两种情形a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°;b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.分别列出方程求解即可.
试题解析:
解:(1)∵y=﹣x+10的图象交x轴于点A,交y轴于点B,
∴A(10,0),B(0,10),
∴OA=OB=10,
∵∠AOB=90°,
∴∠OAB=∠OBA=45°,
故答案分别为(10,0),(0,10),45°.
(2)由题意P(1+2t,0),⊙O半径为1+t,
故答案分别为(1+2t,0),1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.
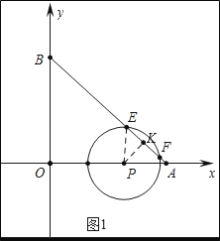
当t=![]() 时,P(6,0),半径为3.5,
时,P(6,0),半径为3.5,
在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,
∴PK=![]() ,PA=2
,PA=2![]() ,
,
在Rt△PEK中,EK=![]() =
=![]() ,
,
∴EF=2EK=![]() .
.
②存在.
a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°
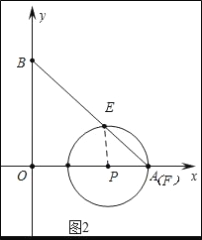
∵OP+PA=OA,
∴1+2t+1+t=10,
∴t=![]() .
.
b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.
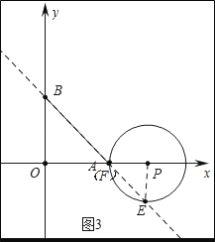
由OP﹣PF=OA,
∴1+2t﹣(1+t)=10,
∴t=10,
综上所述,t=![]() s或10s时,存在以点P为直角顶点的Rt△PEF.
s或10s时,存在以点P为直角顶点的Rt△PEF.

 通城学典默写能手系列答案
通城学典默写能手系列答案