题目内容
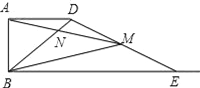
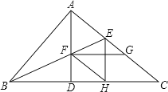
【题目】如图在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,BE为∠ABC的角平分线交AC于E,交AD于F,FG∥BD,交AC于G,过E作EH⊥CD于H,连接FH,下列结论:①四边形CHFG是平行四边形,②AE=CG,③FE=FD,④四边形AFHE是菱形,其中正确的是( )
A.①②③④ B.②③④ C.①③④ D.①②④
【答案】D
【解析】
试题分析:因为BE为∠ABC的角平分线,∠BAC=90°,EH⊥CD,所以AE=EH,又因为AD是斜边BC上的高,所以∠FBD+∠BFD=90°,∠ABF+∠AEB=90°,所以∠BFD=∠AEB,所以∠AFE=∠AEB,所以AF=AE,所以AF=EH,又因为EH∥AD,所以四边形AEHF是平行四边形,因为AE=EH可得四边形AEHF是菱形,所以④正确;所以FH∥AC,所以四边形CHFG是平行四边形,①正确;所以CG=FH=AE,②正确;而③中EF与FD并不存在相等,所以①②④正确,故选:D.

练习册系列答案
相关题目