题目内容
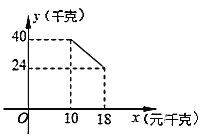
【题目】已知抛物线y＝ax2﹣4ax+3a交x轴于A、B两点（点A在点B左侧），且抛物线顶点的纵坐标为﹣1．
（1）求抛物线的解析式；
（2）若P是抛物线上一点，过点P作PQ⊥x轴交直线l1：y＝x+t于点Q．若恰好存在三个点P使得PQ＝
，求证：直线l1过点A；
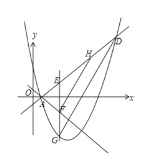
（3）在（2）的结论下，直线l1与抛物线的另一个交点为D，直线l2：y＝kx+c（﹣4＜k＜﹣1）经过点A，过线段AD上一点E（异于点A、D）作x轴的垂线，分别与直l2、抛物线交于点F、G．连接GD，作FH∥GD交直线l1于点H，求EH长的取值范围．
【答案】（1）y＝x2﹣4x+3；（2）见解析；（3）EH长的取值范围为：2
＜EH＜5．
【解析】
（1）y＝ax2﹣4ax+3a＝a（x2﹣4x+3），则点A、B的坐标为：（1，0）、（3，0），则函数的对称轴为：x＝2，顶点为：（2，1），即可求解；
（2）恰好存在三个点P使得PQ＝
，则出现如图所示的情况，点Q在点P的上方只有一个，如图P、Q点所示的情况，设点P（x，x2﹣4x+3），则点Q（x，x+t），PQ＝x+t﹣（x2﹣4x+3）＝﹣x2+5x+t﹣3，因为1＜0，故PQ有最大值，此时
，代入PQ，解得t的值，即可求解；
（3）设点E（m，m﹣1），则点G（m，m2﹣4m+3），点F（m，mk﹣k），点D（4，3），求出直线HF的表达式，联立①②并解得：x＝m＋1k＝
，求出EH，根据4＜k＜1，即可求得解．
（1）y＝ax2﹣4ax+3a＝a（x2﹣4x+3），
则点A、B的坐标为：（1，0）、（3，0），
则函数的对称轴为：x＝2，顶点为：（2，﹣1），
则y＝a（x﹣2）2﹣1＝ax2﹣4ax+4a﹣1，
故3a＝4a﹣1，解得：a＝1，
故抛物线的表达式为：y＝x2﹣4x+3；
（2）恰好存在三个点P使得PQ＝，则出现如图所示的情况，
点Q在点P的上方只有一个，如图P、Q点所示的情况，
设点P（x，x2﹣4x+3），则点Q（x，x+t），
PQ＝x+t﹣（x2﹣4x+3）＝﹣x2+5x+t﹣3，
∵﹣1＜0，故PQ有最大值，此时，
则
，解得：t＝﹣1，
即y＝x﹣1，当x＝1时，y＝0，
所以直线l1过点A；
（3）将点A的坐标代入直线l2的表达式并解得：
直线l2的表达式为：y＝kx﹣k，
直线l1的表达式为：y＝x﹣1…①，
设点E（m，m﹣1），则点G（m，m2﹣4m+3），点F（m，mk﹣k），点D（4，3），
将点G、D的坐标代入一次函数表达式得：直线GD表达式中的k值为：
，
FH∥GD，则设直线FH的表达式为：y＝mx+b，
将点F的坐标代入上式并解得：
直线HF的表达式为：y＝mx+（mk﹣k﹣m2）…②，
联立①②并解得：x＝m+1﹣k＝，
则EH＝（
）＝（m+1﹣k﹣m）＝（1﹣k），
而﹣4＜k＜﹣1，则2＜EH＜5；
故EH长的取值范围为：2＜EH＜5．
