Question

【题目】如图，△ABC中，AB＝3，AC＝4，以AC为斜边向外作等腰直角△ACD．连接BD，将△DAB绕点D顺时针旋转90°，点B的对应点为E．

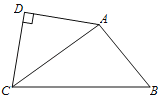
（1）画出旋转后的三角形；

（2）在（1）的情况下连接BE，若BC＝5，求△BCE的面积．

Answer 1

【答案】（1）旋转后的△DEC即为所求．见解析；（2）S△BEC＝．

【解析】

（1）根据要求画出图形即可解决问题．
（2）利用勾股定理逆定理证明∠CAB＝90°，再证明E，C，A共线即可解决问题．

（1）旋转后的△DEC即为所求．

（2）∵AC＝4，AB＝3，BC＝5，

∴AB2+AC2＝BC2，

∴∠CAB＝90°，

∵DC＝AD，∠CDA＝90°，

∴∠DCA＝∠DAC＝45°，

∴∠DAB＝∠DAC+∠CAB＝45°+90°＝135°，

∵∠DCE＝∠DAB＝135°，

∴∠DCE+∠DCA＝180°，

∴E，C，A共线，

∴S△BEC＝ECBA＝×3×3＝．