题目内容
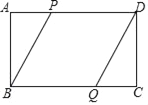
【题目】如图,平面直角坐标系中有4个点:A(0,2),B(﹣2,﹣2),C(﹣2,2),D(3,3).
(1)在正方形网格中画出△ABC的外接圆⊙M,圆心M的坐标是 ;
(2)若EF是⊙M的一条长为4的弦,点G为弦EF的中点,求DG的最大值;
(3)点P在直线MB上,若⊙M上存在一点Q,使得P、Q两点间距离小于1,直接写出点P横坐标的取值范围.

【答案】(1)(-1,0);(2)6;(3)﹣![]() <x<
<x<![]() 或﹣2﹣
或﹣2﹣![]() <x<﹣2+
<x<﹣2+![]() ;
;
【解析】
(1)画出△ABC的外接圆即可解决问题;
(2)当点G在线段DM延长线上时DG最大,此时DG=DM+GM,
(3)分两种情形构建方程即可即可解决问题;
(1)如图所示;M(-1,0);
故答案为(-1,0).
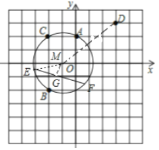
(2)连接MD,MG,ME,
∵点G为弦EF的中点,EM=FM=![]() ,
,
∴MG⊥EF,
∵EF=4,
∴EG=FG=2,
∴MG=![]() =1,
=1,
∴点G在以M为圆心,1为半径的圆上,
∴当点G在线段DM延长线上时DG最大,此时DG=DM+GM,
∵DM=![]() =5,
=5,
∴DG的最大值为5+1=6;
(3)设P点的横坐标为x,
当P点位于线段MB及延长线上且P、Q两点间距离等于1,时,![]() ,
,
∴![]() 或
或![]()
解得|xp|=2+![]() 或2-
或2-![]() ,
,
∵此时P点在第三象限,
∴x<0,
∴x=-2-![]() 或-2+
或-2+![]() ,
,
即当P、Q两点间距离小于1时点P横坐标的取值范围为-2-![]() <x<-2+
<x<-2+![]() ;
;
当P点位于线段BM及延长线上且P、Q两点间距离等于1时,则PQ:AM=|x|:|xM|,
![]() ,
,
解得|x|=![]() ,
,
∵此时P点在第一或二象限,
∴x=±![]() ,
,
即当P、Q两点间距离小于1时点P横坐标的取值范围为-![]() <x
<x![]() ;
;
综上所述,点P横坐标的取值范围为-![]() <x
<x![]() 或-2-
或-2-![]() <x<-2+
<x<-2+![]() .
.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】阅读可以增进人们的知识也能陶治人们的情操。我们要多阅读,多阅读有营养的书。因此我校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,整理后的数据如下表(表中信息不完整)。图1和图2是根据整理后的数据绘制的两幅不完整的统计图.
阅读时间分组统计表 | ||
组别 | 阅读时间x(h) | 人数 |
A |
| a |
B |
| 100 |
C |
| b |
D |
| 140 |
E |
| c |
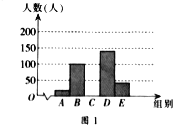
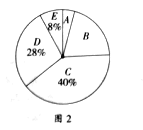
请结合以上信息解答下列问题
(1)求a,b,c的值;
(2)补全图1所对应的统计图;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.