题目内容
【题目】在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,

(1)求∠AOC的度数
(2)连接BO,试说明BO平分∠ABC
(3)判断AC、AE、CD的关系,并说明理由.
【答案】(1)120°;(2)详见解析;(3)AC=AE+CD
【解析】
(1)根据三角形的内角和等于180°求出![]() ,再根据角平分线的定义求出
,再根据角平分线的定义求出![]() ,然后根基三角形的内角和等于180°列式计算即可得解;
,然后根基三角形的内角和等于180°列式计算即可得解;
(2)作垂线,由角平分线定理即可得证.
(3)通过角之间的转化可得出△COD和△COF全等,进而可得出线段之间的关系,即可得出结论.
(1)∵∠ABC=60°,
∴![]() ,
,
∵AD,CE分别平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]()
![]()
![]() .
.
(2)如图,连接OB,作OM⊥AB于点M,ON⊥AC于点N,OG⊥BC于点G,
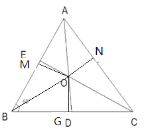
∵AD,CE分别平分![]() ,
,
∴OM=ON,ON=OG,
∴OM=OG,
由角平分线定理,
∴BO平分∠ABC.
(3)如图,在AC上截取AF=AE,
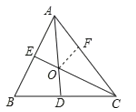
∵AD平分![]() ,
,
∴![]() ,
,
在△AOE和△AOF中,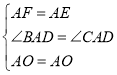 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() (对顶角相等),
(对顶角相等),
∴![]() ,
,
∵CE平分![]() ,
,
∴![]() ,
,
在△COD和△COF中,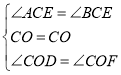 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目









