题目内容
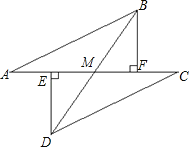
【题目】如图,点E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.求证:
(1)AB∥CD;
(2)点M是线段EF的中点.
【答案】(1)见解析;(2)见解析.
【解析】
(1)证明Rt△ABF≌Rt△CDE可得∠BAF=∠DCE,即可得出结论;
(2)可证明△DEM≌△BFM,即可得出结论.
(1)∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,
![]() ,
,
∴Rt△ABF≌Rt△CDE(HL),
∴∠BAF=∠DCE,
∴AB∥CD;
(2)∵Rt△ABF≌Rt△CDE,
∴DE=BF,
在△DEM和△BFM中,
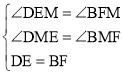 ,
,
∴△DEM≌△BFM(AAS),
∴MB=MD.
即点M是线段EF的中点.

练习册系列答案
相关题目
【题目】为了了解某校学生的身高状况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制如图所示的统计图表:
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
已知女生身高在A组的有8人,根据图表中提供的信息,回答下列问题:
(1)男生身高的中位数落在 组(填组别字母序号);
(2)在样本中,身高在150≤x<155之间的人数共有 人,身高人数最多的在 组(填组别序号);
(3)已知该校共有男生400人、女生420人,请估计身高不足160cm的学生约有多少人?