题目内容
【题目】已知:如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 点和
点和![]() 点(
点(![]() 点在
点在![]() 点左则),交
点左则),交![]() 轴于
轴于![]() 点,作直线
点,作直线![]() 是直线
是直线![]() 上方抛物线上的一个动点.过
上方抛物线上的一个动点.过![]() 点作 直线
点作 直线![]() 平行于直线
平行于直线![]() 是直线
是直线 ![]() 上的任意点,
上的任意点,![]() 是直线
是直线![]() 上的任意点,连接
上的任意点,连接![]() ,始终保持
,始终保持![]() 为
为![]() ,以
,以![]() 和
和![]() 边,作矩形
边,作矩形![]() .
.
(1)在![]() 点移动过程中,求出当
点移动过程中,求出当![]() 的面积最大时点
的面积最大时点![]() 的坐标;在
的坐标;在![]() 的面积最大 时,求矩形
的面积最大 时,求矩形![]() 的面积的最小值.
的面积的最小值.
(2)在![]() 的面积最大时,线段
的面积最大时,线段![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 四个点组成平行 四边形时,求此时线段
四个点组成平行 四边形时,求此时线段![]() 与抛物线的交点坐标.
与抛物线的交点坐标.
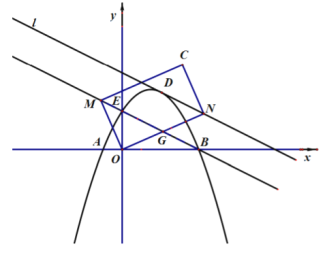
【答案】(1)![]() 点坐标为
点坐标为![]() ,矩形
,矩形![]() 的最小值为
的最小值为![]() ;(2)交点坐标为(3+
;(2)交点坐标为(3+![]() ,﹣
,﹣![]() ),(3﹣
),(3﹣![]() ,﹣
,﹣![]() ),(1﹣
),(1﹣![]() ,
,![]() ),(1+
),(1+![]() ,
,![]() ).
).
【解析】
(1)当△DEB的面积最大时,直线DN与抛物线相切,可求出直线DN的解析式和点D的坐标,当矩形面积最小时,MG最小,求出MG的最小值即可.
(2)分两种情况讨论,以DB为边和以DB为对角线,分别求出此时ON的解析式,联立求出交点坐标即可.
解:(1)如图1所示,过点D作y轴的平行线交MB于点H,过点O作OQ垂直MB于点Q,
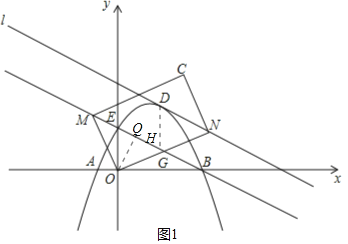
令y=0,解得x1=﹣1,x2=4,
∴A(﹣1,0),B(4,0),
令x=0,y=2,
∴E(0,2),
设直线BE的解析式为y=kx+b,则![]()
解得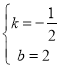 ,
,
∴直线BE的解析式为y=﹣![]() x+2,
x+2,
∵DN∥BE,
∴设直线DN的解析式为y=﹣![]() x+b1,
x+b1,
S△DEB=DH![]() (xB﹣xE),
(xB﹣xE),
∴当△DEB面积最大时,即是DH最大的时候,
∴﹣![]() x+b1=﹣
x+b1=﹣![]() x2+
x2+![]() x+2,
x+2,
△=b2﹣4ac=0,即16﹣4(2b1﹣4)=0,
解得b1=4,点D(2,3),
S矩=2S△MOG+S平形四边形,
∴矩形面积最小时就是MG最小,
设QG=m,MQ=n,
∴MG=m+n,
∵m+n≥2![]() ,
,
∵△QOG∽△MQO,
∴OQ2=mn,
∵△OEQ∽△EOB,
∴OQ=![]() ,
,
∴mn=![]() ,
,
∴m+n的最小值为![]() .
.
∴MG=![]() ,
,
∴S矩=2S△MOG+S平形四边形=![]() .
.
(2)分两种情况讨论,
情况一:当GN∥DB时,
直线DB的解析式为:y=﹣![]() x+6,
x+6,
则直线NG的解析式为y=﹣![]() x,
x,
∴﹣![]() x=﹣
x=﹣![]() x2+
x2+![]() x+2,
x+2,
解得x1=3+![]() ,x2=3﹣
,x2=3﹣![]() ,
,
∴交点坐标为(3+![]() ,﹣
,﹣![]() ),(3﹣
),(3﹣![]() ,﹣
,﹣![]() ),
),
情况二:DB为对角线时,此时NG必过DB的中点(3,![]() ),
),
设直线ON的解析式为y=k1x,
则k1=![]() ,
,
∴直线OD的解析式为y=![]() x,
x,
![]() =﹣
=﹣![]() x2+
x2+![]() x+2,
x+2,
解得x1=1﹣![]() ,x2=1+
,x2=1+![]() ,
,
∴交点坐标为(1﹣![]() ,
,![]() ),(1+
),(1+![]() ,
,![]() ),
),
综上所述:交点坐标为(3+![]() ,﹣
,﹣![]() ),(3﹣
),(3﹣![]() ,﹣
,﹣![]() ),(1﹣
),(1﹣![]() ,
,![]() ),(1+
),(1+![]() ,
,![]() ).
).

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案【题目】距离中考体育考试时间越来越近,某校想了解初三年级1500名学生跳绳情况,从中随机抽查了20名男生和20名女生的跳绳成绩,收集到了以下数据:
男生:192、166,189,186,184,182,178,177,174,170,188,168,205,165,158,150,188,172,180,188
女生:186,198,162,192,188,186,185,184,180,180,186,193,178,175,172,166,155,183,187,184.
根据统计数据制作了如下统计表:
个数x | 150≤x<170 | 170≤x<185 | 185≤x<190 | x≥190 |
男生 | 5 | 8 | 5 | 2 |
女生 | 3 | 8 | a | 3 |
两组数据的极差、平均数、中位数、众数如表所示:
极差 | 平均数 | 中位数 | 众数 | |
男生 | 55 | 178 | b | c |
女生 | 43 | 181 | 184 | 186 |
(1)请将上面两个表格补充完整:a=____,b=_____,c=_____;
(2)请根据抽样调查的数据估计该校初三年级学生中考跳绳成绩能得满分(185个及以上)的同学大约能有多少人?
(3)体育组的江老师看了表格数据后认为初三年级的女生跳绳成绩比男生好,请你结合统计数据,写出支持江老师观点的理由.