ЬтФПФкШн
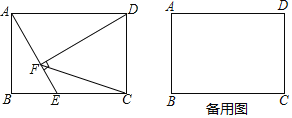
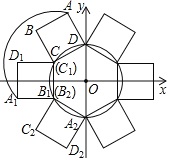
ЁОЬтФПЁПШчЭМЃЌЁбOЕФАыОЖЮЊ2ЃЌдВаФOдкзјБъдЕуЃЌе§ЗНаЮABCDЕФБпГЄЮЊ2ЃЌЕуAЁЂBдкЕкЖўЯѓЯоЃЌЕуCЁЂDдкЁбOЩЯЃЌЧвЕуDЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЌЯжНЋе§ЗНаЮABCDШЦЕуCАДФцЪБеыЗНЯђа§зЊ150ЁуЃЌЕуBдЫЖЏЕНСЫЁбOЩЯЕуB1ДІЃЌЕуAЁЂDЗжБ№дЫЖЏЕНСЫЕуA1ЁЂD1ДІЃЌМДЕУЕНе§ЗНаЮA1B1C1D1ЃЈЕуC1гыCжиКЯЃЉЃЛдйНЋе§ЗНаЮA1B1C1D1ШЦЕуB1АДФцЪБеыЗНЯђа§зЊ150ЁуЃЌЕуA1дЫЖЏЕНСЫЁбOЩЯЕуA2ДІЃЌЕуD1ЁЂC1ЗжБ№дЫЖЏЕНСЫЕуD2ЁЂC2ДІЃЌМДЕУЕНе§ЗНаЮA2B2C2D2ЃЈЕуB2гыB1жиКЯЃЉЃЌЁЃЌАДЩЯЪіЗНЗЈа§зЊ2020ДЮКѓЃЌЕуA2020ЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A.ЃЈ0ЃЌ2ЃЉB.ЃЈ2+![]() ЃЌЉ1ЃЉ
ЃЌЉ1ЃЉ
C.ЃЈЉ1Љ![]() ЃЌЉ1Љ
ЃЌЉ1Љ![]() ЃЉD.ЃЈ1ЃЌЉ2Љ
ЃЉD.ЃЈ1ЃЌЉ2Љ![]() ЃЉ
ЃЉ
ЁОД№АИЁПB
ЁОНтЮіЁП
ИљОнЬтвтевЕНЙцТЩЃЌ12ДЮЮЊвЛИібЛЗЃЌдђA2020ЕФзјБъгыA4ЯрЭЌЃЌЧѓГіA4ЕФзјБъМДПЩНтОіБОЬт.
НтЃКШчЭМЃЌгЩЬтвтЗЂЯж12ДЮвЛИібЛЗЃЌ

Ёп2020ЁТ12ЃН168![]() ЃЌ
ЃЌ
ЁрA2020ЕФзјБъгыA4ЯрЭЌЃЌ
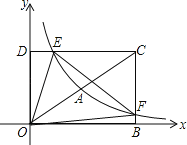
ШчЭМЃЌСЌНгM A4ЁЂOEЁЂOFЃЌ
ЁрЁЯEOF=360ЁТ6=60ЁуЃЌ
ЁпOE=OEЃЌ
ЁрЁїOEFЮЊЕШБпШ§НЧаЮЃЌ
ЁрЁЯOEF=60ЁуЃЌЁЯOME=90ЁуЃЌ
ЁрOM=OEЁСcos60Ёу=![]() ЃЌMF=
ЃЌMF=![]() ЃЌ
ЃЌ
ЁрON=OM+MN=2+![]() ЃЌNA=MF=1ЃЌ
ЃЌNA=MF=1ЃЌ
ЁрA4ЃЈ2+![]() ЃЌЉ1ЃЉЃЌ
ЃЌЉ1ЃЉЃЌ
ЁрA2020ЃЈ2+![]() ЃЌЉ1ЃЉЃЌ
ЃЌЉ1ЃЉЃЌ
ЙЪбЁЃКBЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ