题目内容
(本题满分10分)
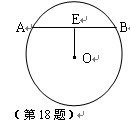
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且PD∥CB,弦PB与CD交于点F
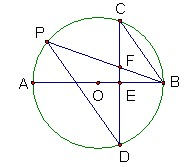
(1)求证:FC=FB;
(2)若CD=24,BE=8,求⊙O的直径
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且PD∥CB,弦PB与CD交于点F

(1)求证:FC=FB;
(2)若CD=24,BE=8,求⊙O的直径
(1)证明略
(2)26
(1)证明:∵PD∥CB,∴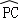 =
=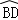 ,∴∠FBC=∠FCB,∴FC=FB.
,∴∠FBC=∠FCB,∴FC=FB.
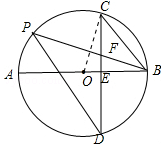
(2)解:如图:连接OC,设圆的半径为r,在Rt△OCE中,
OC=r,OE=r﹣8,CE=12,∴r2=(r﹣8)2+122,
解方程得:r=13.
所以⊙O的直径为26.
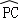 =
=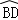 ,∴∠FBC=∠FCB,∴FC=FB.
,∴∠FBC=∠FCB,∴FC=FB.(2)解:如图:连接OC,设圆的半径为r,在Rt△OCE中,
OC=r,OE=r﹣8,CE=12,∴r2=(r﹣8)2+122,
解方程得:r=13.
所以⊙O的直径为26.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 cm
cm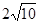 cm
cm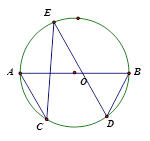
 的直径
的直径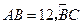 的长为2
的长为2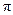 ,
,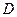 在
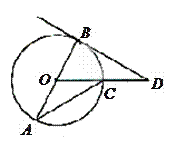
在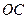 的延长线上,且
的延长线上,且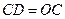 .
.
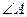 的度数;
的度数;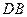 是
是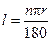 ,其中
,其中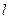 是弧长,
是弧长,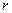 是半径,
是半径,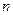 是圆心角度数)
是圆心角度数)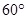 ,则该弧所在的圆的半径为 ( )
,则该弧所在的圆的半径为 ( )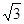
 外接圆,
外接圆, ,BD为⊙
,BD为⊙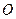 的直径,BD=2,连结CD,求BC的长
的直径,BD=2,连结CD,求BC的长