Question

【题目】设函数（其中k为常数）.

（1）当k=-2时，函数y存在最值吗？若存在，请求出这个最值；

（2）在x＞0时，要使函数y的的值随x的增大而减小，求k应满足的条件；

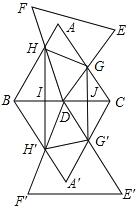
（3）若函数y的图象与x轴交于A、B两点，与y轴交于点C，求能使△ABC为等腰三角形的k的值.（分母保留根号，不必化简）

Answer 1

【答案】（1）x=-时，y最大=；（2）k≤0；（3）k=3,k=，k=,k=-.

【解析】

试题分析：本题考查二次函数的有关知识、一次函数的有关知识，掌握函数的性质是解决问题的关键，学会分类讨论的思想，属于中考常考题型．

（1）把k=-2代入抛物线解析式得到y=-2x2-5x-3，根据顶点坐标公式即可解决．

（2）分两种情形讨论当k=0时，y=-3x-3为一次函数，k=-3＜0，则当x＞0时，y随x的增大而减小；当k≠0时，y=（kx-3）（x+1）=kx2+（k-3）x-3为二次函数，由不等式组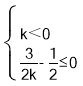解决．

（3）分三种情形讨论：当k＞0时①AC=BC，②AC=AB，③AB=BC分别列出方程解决；当k＜0时，B只能在A的左侧，只有AC=AB列出方程解决，当k=0时，不合题意．

试题解析：（1）当k=-2时，函数y=（-2x-3）（x+1）=-（2x+3）（x+1），

函数为二次函数，且二次项系数小于0，故函数存在最大值，

当x=-时，y最大=；

（2）当k=0时，y=-3x-3为一次函数，-3＜0，则当x＞0时，y随x的增大而减小；

当k≠0时，y=（kx-3）（x+1）为二次函数，其对称轴为直线x==-，要使当x＞0时，y随x的增大而减小，则抛物线的开口必定朝下，且对称轴不在y轴的右边.

故得，，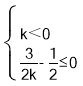

解得k＜0,

综上所述，k应满足的条件是：k≤0.

（3）由题意得，k≠0，函数为二次函数.

由所给的抛物线解析式可得A，C为定值A（-1,0），C（0，-3）则AC=，而B（，0）,

（1）k＞0，则可得,

①AC=BC，则有=，可得k=3,

②AC=AB，则有+1=，可得k=，

③AB=BC，则有+1=，可得k=,

④k＜0，B只能在A的左侧,

只有AC=AB，则有--1=，可得k=-.