题目内容
【题目】如图,有一条两岸平行的河流,一数学实践活动小组在无法涉水过河情况下,成功测得河的宽度,他们的做法如下:
①正对河流对岸的一颗树A,在河的一岸选定一点B;
②沿河岸直走15步恰好到达一树C处,继续前行15步到达D处;
③自D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时,停止行走;
④测得DE的长就是河宽.
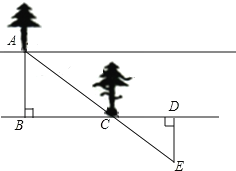
请你运用所学知识说明他们做法是正确的.
【答案】说明见解析.
【解析】根据AB⊥BD,ED⊥BD可知∠ABC=∠EDC,再由BC=DC,∠ACB=∠ECD可得出△ABE≌△EDC,由全等三角形的性质即可得出结论.
解:∵AB⊥BD,ED⊥BD,∴∠ABC=∠EDC=90°.
在△ABC与△EDC中,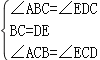 ,∴△ABC≌△EDC(ASA),
,∴△ABC≌△EDC(ASA),
∴DE=AB,即测得DE的长就是河宽.
“点睛”本题考查的是全等三角形的判定与性质,熟知全等三角形的对应边相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目