Question

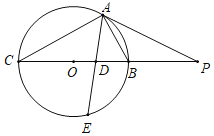
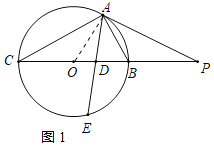
【题目】如图，△ABC内接于⊙O，BC为直径，∠BAC的平分线与BC和⊙O分别相交于D和E，P为CB延长线上一点，PB＝5，PA＝10，且∠DAP＝∠ADP．

（1）求证：PA与⊙O相切；

（2）求sin∠BAP的值；

（3）求ADAE的值．

Answer 1

【答案】（1）详见解析；（2）；（3）90.

【解析】

（1）连接OA，由三角形的外角性质和角平分线得出∠PAB＝∠C，由等腰三角形的性质得出∠OAC＝∠C＝∠PAB，由圆周角定理得出∠BAC＝90°，证出∠OAP＝90°，即AP⊥OA，即可得出PA与⊙O相切；

（2）证明△PAB∽△PCA，得出 得出，即可得出结果；

（3）连接CE，由切割线定理求出PC＝20，得出BC＝PC﹣PB＝15，求出，再证明△ACE∽△ADB，得出，即可得出结果．

（1）证明：连接OA，如图1所示：

∵AE平分∠BAC，

∴∠BAD＝∠CAD，

∵∠DAP＝∠BAD+∠PAB，∠ADP＝∠CAD+∠C，∠DAP＝∠ADP，

∴∠PAB＝∠C，

∵OA＝OC，

∴∠OAC＝∠C＝∠PAB，

∵BC为直径，

∴∠BAC＝90°，即∠OAC+∠OAB＝90°，

∴∠PAB+∠OAB＝90°，即∠OAP＝90°，

∴AP⊥OA，

∴PA与⊙O相切；

（2）解：∵∠P＝∠P，∠PAB＝∠C，

∴△PAB∽△PCA，

∴

∵∠CAB＝90°，

∴

∴sin∠BAP＝sin∠C＝；

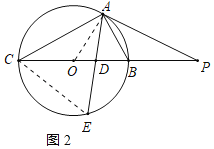
（3）解：连接CE，如图2所示：

∵PA与⊙O相切，

∴PA2＝PB×PC，即102＝5×PC，

∴PC＝20，

∴BC＝PC﹣PB＝15，

∵

∴，

∵AE是∠BAC的角平分线，

∴∠BAD＝∠CAE，

∵∠E＝∠ABD，

∴△ACE∽△ADB，

∴

∴